题目内容
【题目】如图，四边形ABCD为矩形纸片，把纸片ABCD折叠，使点B恰好落在边DC的中点E，折痕为AF，已知CD=8cm．求：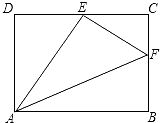 
（1）AD的长；
（2）△ABF的面积．
【答案】
（1）解：∵四边形ABCD为矩形，
∴∠D=90°，BC=AD；
由题意得：AE=AB=CD=8，DE=EC=4；BF=EF（设为λ）；
由勾股定理得：AD2=AE2﹣DE2，
∴AD= 
（cm）．
（2）解：由（1）知：BC=AD=4 
，BF=EF（设为λ）；
则CF=4 ﹣λ；由勾股定理得：
，解得：λ= 
，
∴△ABF的面积= 
×8× = 
（cm2）．
【解析】（1）证明AE=AB=8，DE=EC=4，运用勾股定理即可解决问题．（2）证明BF=EF（设为λ）此为解决问题的关键性结论；借助勾股定理列出关于BF的方程，即可解决问题．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
相关题目
