题目内容
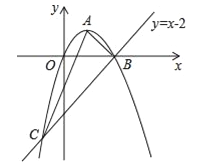
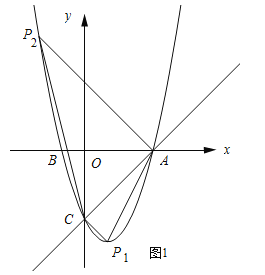
【题目】如图，在平面直角坐标系中，已知抛物线
过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，﹣3），动点P在抛物线上．
（1）b= ，c= ，点B的坐标为 ；（直接填写结果）
（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．
【答案】（1）b=﹣2，c=﹣3，B（﹣1，0）；（2）P（1，﹣4）或（﹣2，5）；（3）（
，
）或（
，）．
【解析】
试题分析：（1）将点A和点C的坐标代入抛物线的解析式可求得b、c的值，然后令y=0可求得点B的坐标；
（2）分别过点C和点A作AC的垂线，将抛物线与P1，P2两点先求得AC的解析式，然后可求得P1C和P2A的解析式，最后再求得P1C和P2A与抛物线的交点坐标即可；
（3）连接OD．先证明四边形OEDF为矩形，从而得到OD=EF，然后根据垂线段最短可求得点D的纵坐标，从而得到点P的纵坐标，然后由抛物线的解析式可求得点P的坐标．
试题解析：（1）∵将点A和点C的坐标代入抛物线的解析式得：
，解得：b=﹣2，c=﹣3，∴抛物线的解析式为
．∵令
，解得：
，
，∴点B的坐标为（﹣1，0）．故答案为：﹣2；﹣3；（﹣1，0）．
（2）存在．理由：如图所示：
①当∠ACP1=90°．由（1）可知点A的坐标为（3，0）．设AC的解析式为y=kx﹣3．
∵将点A的坐标代入得3k﹣3=0，解得k=1，∴直线AC的解析式为y=x﹣3，∴直线CP1的解析式为y=﹣x﹣3．∵将y=﹣x﹣3与联立解得
，
（舍去），∴点P1的坐标为（1，﹣4）．
②当∠P2AC=90°时．设AP2的解析式为y=﹣x+b．∵将x=3，y=0代入得：﹣3+b=0，解得b=3，∴直线AP2的解析式为y=﹣x+3．∵将y=﹣x+3与联立解得
=﹣2，
=3（舍去），∴点P2的坐标为（﹣2，5）．
综上所述，P的坐标是（1，﹣4）或（﹣2，5）．
（3）如图2所示：连接OD．
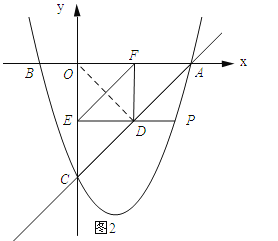
由题意可知，四边形OFDE是矩形，则OD=EF．根据垂线段最短，可得当OD⊥AC时，OD最短，即EF最短．
由（1）可知，在Rt△AOC中，∵OC=OA=3，OD⊥AC，∴D是AC的中点．又∵DF∥OC，∴DF=
OC=
，∴点P的纵坐标是，∴
，解得：x=
，∴当EF最短时，点P的坐标是：（，）或（，）．
