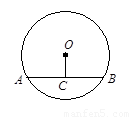题目内容
半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC∶CA = 4∶3,点P在⊙O上运动,过点C作CP的垂线,与PB的延长线交于点Q.


(1)当点P运动到与点C关于AB对称时,求CQ的长;
(2)当点P运动到弧CP的中点时,求CQ的长.
(3)当点P运动到什么位置时,CQ取到最大值,并求此时CQ的长.
解:(1)当点P运动到与点C关于AB对称时,如图所示,此时CP⊥AB于D,
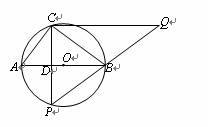
又∵AB为⊙O的直径, ∴∠ACB =90°.
∵AB=5, BC∶CA=4∶3, ∴BC = 4, AC=3.
又∵AC?BC=AB?CD, ∴ ![]() ,
, ![]() .
.
在Rt△PCQ中,∠PCQ = 90°, ∠CPQ =∠CAB,
∴![]() .
.
∴![]() .
.
(2) 当点P运动到弧CP的中点时,如图所示,过点B作BE⊥PC于点E,
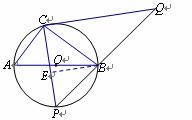
∵P是弧AB的中点, ∠PCB=45°, ∴![]() .
.
又∠CPB=∠CAB, ∴tan∠CPB= tan∠CAB=![]() ,
,
即![]()
![]() , 从而
, 从而![]() .
.
由(1)得,![]() .
.
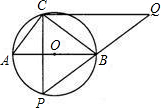
(3)因为点P在⊙O上运动过程中,在Rt△PCQ中,有![]() .
.
所以PC最大时,CQ取到最大值.
∴当PC过圆心O,即PC 取最大值 5时,CQ最大,最大为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在半径为13厘米的圆中,弦AB与弦CD平行.AB=24厘米,CD=10厘米,则两弦的距离为( )
| A、17厘米 | B、12厘米 | C、7厘米 | D、7厘米或17厘米 |
 如图,在半径为6 cm的⊙O中,圆心O到弦AB的距离OC为3 cm.试求:
如图,在半径为6 cm的⊙O中,圆心O到弦AB的距离OC为3 cm.试求:
 半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC:CA=4:3,点P在
半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC:CA=4:3,点P在