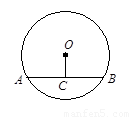题目内容
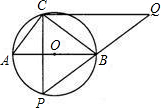 半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC:CA=4:3,点P在
半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC:CA=4:3,点P在 |
| AB |
(1)当点P与点C关于AB对称时,求CQ的长;
(2)当点P运动到
 |
| AB |
(3)当点P运动到什么位置时,CQ取到最大值?求此时CQ的长.
分析:(1)如果点P与点C关于AB对称,根据垂径定理可得出CP⊥AB,在直角三角形ABC中,根据△ABC面积的不同表示方法可求出CD的长,即可得出PC的值,进而可通过相似三角形△PQC和△ABC(∠A=∠P,一组直角)求出CQ的长.
(2)当点P运动到弧AB的中点时,过点B作BE⊥PC于点E(如图);由于P是弧AB的中点,由圆周角定理得∠ACP=∠PCB=45°,由△CEB是等腰直角三角形,可得CE=BE=
BC=2
;又由圆周角定理得∠CPB=∠CAB,由正切的概念知tan∠CPB=tan∠CAB=
=BE:PE,得到PE=
=
BE=
进而求得PC,而从(1)中得,CQ=
PC=
.
(3)如果CQ去最大值,那么PC也应该取最大值,因此当PC是圆O的直径时,CQ才取最大值.此时PC为5,可根据上面得出的PC、CQ的比例关系求出CQ的长.
(2)当点P运动到弧AB的中点时,过点B作BE⊥PC于点E(如图);由于P是弧AB的中点,由圆周角定理得∠ACP=∠PCB=45°,由△CEB是等腰直角三角形,可得CE=BE=
| ||
| 2 |
| 2 |
| 4 |
| 3 |
| BE |
| tan∠CPB |
| 3 |
| 4 |
3
| ||
| 2 |
| 4 |
| 3 |
14
| ||
| 3 |
(3)如果CQ去最大值,那么PC也应该取最大值,因此当PC是圆O的直径时,CQ才取最大值.此时PC为5,可根据上面得出的PC、CQ的比例关系求出CQ的长.
解答: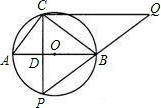 解:(1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D.
解:(1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D.
∵AB为⊙O的直径,
∴∠ACB=90°.
∴AB=5,又∵BC:CA=4:3,
∴BC=4,AC=3.
又∵
AC•BC=
AB•CD
∴CD=
,PC=
在Rt△ACB和Rt△PCQ中,
∠ACB=∠PCQ=90°,∠CAB=∠CPQ,
Rt△ACB∽Rt△PCQ
∴
=
,
∴CQ=
=
PC=
.
(2)当点P运动到弧AB的中点时,过点B作BE⊥PC于点E(如图).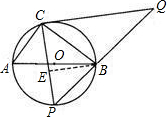
∵P是弧AB的中点,
∴∠PCB=45°,CE=BE=
BC=2
又∠CPB=∠CAB
∴tan∠CPB=tan∠CAB=
∴PE=
=
BE=
,PC=
而从(1)中得,CQ=
PC=
.
(3)点P在弧AB上运动时,恒有CQ=
=
PC;
故PC最大时,CQ取到最大值.
当PC过圆心O,即PC取最大值5时,CQ最大值为
.
 解:(1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D.
解:(1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D.∵AB为⊙O的直径,
∴∠ACB=90°.
∴AB=5,又∵BC:CA=4:3,
∴BC=4,AC=3.
又∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| 12 |
| 5 |
| 24 |
| 5 |
在Rt△ACB和Rt△PCQ中,
∠ACB=∠PCQ=90°,∠CAB=∠CPQ,
Rt△ACB∽Rt△PCQ
∴
| AC |
| BC |
| PC |
| CQ |
∴CQ=
| BC•PC |
| AC |
| 4 |
| 3 |
| 32 |
| 5 |
(2)当点P运动到弧AB的中点时,过点B作BE⊥PC于点E(如图).

∵P是弧AB的中点,
∴∠PCB=45°,CE=BE=
| ||
| 2 |
| 2 |
又∠CPB=∠CAB
∴tan∠CPB=tan∠CAB=
| 4 |
| 3 |
∴PE=
| BE |
| tan∠CPB |
| 3 |
| 4 |
3
| ||
| 2 |
7
| ||
| 2 |
而从(1)中得,CQ=
| 4 |
| 3 |
14
| ||
| 3 |
(3)点P在弧AB上运动时,恒有CQ=
| BC•PC |
| AC |
| 4 |
| 3 |
故PC最大时,CQ取到最大值.
当PC过圆心O,即PC取最大值5时,CQ最大值为
| 20 |
| 3 |
点评:本题属于常规的几何综合题,利用了直角三角形的面积公式,相似三角形的判定和性质,直角三角形的性质,正切的概念求解.解第3小问时要有动态的思想(在草稿上画画图)不难猜想出结论.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
在半径为13厘米的圆中,弦AB与弦CD平行.AB=24厘米,CD=10厘米,则两弦的距离为( )
| A、17厘米 | B、12厘米 | C、7厘米 | D、7厘米或17厘米 |
 如图,在半径为6 cm的⊙O中,圆心O到弦AB的距离OC为3 cm.试求:
如图,在半径为6 cm的⊙O中,圆心O到弦AB的距离OC为3 cm.试求: