题目内容
 如图,在半径为6 cm的⊙O中,圆心O到弦AB的距离OC为3 cm.试求:
如图,在半径为6 cm的⊙O中,圆心O到弦AB的距离OC为3 cm.试求:(1)弦AB的长;
(2)
 | AB |
分析:连接半径,构造直角三角形,利用勾股定理求出AC的长;要求弧长,只要求出它所对的圆心角就可以代入弧长公式求解.
解答: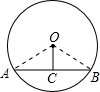 解:(1)连接OA、OB,
解:(1)连接OA、OB,
∵OA=6,OC=3,
∴AC=
=
=3
,(2分)
∵OC⊥AB,
∴AB=2AC=6
;(4分)
(2)∵OA=6,OC=3,
∴∠A=30°,
∴∠AOC=60°,
∴∠AOB=120°,(6分)
的长=
π×6=4π.
 解:(1)连接OA、OB,
解:(1)连接OA、OB,∵OA=6,OC=3,
∴AC=
| OA2-OC2 |
| 62-32 |
| 3 |
∵OC⊥AB,
∴AB=2AC=6
| 3 |
(2)∵OA=6,OC=3,
∴∠A=30°,
∴∠AOC=60°,
∴∠AOB=120°,(6分)
 |
| AB |
| 120 |
| 180 |
点评:本题主要考查作辅助线构造直角三角形,再利用勾股定理计算和弧长公式的记忆.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
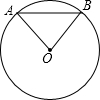 如图,在半径为5的⊙O中,若弦AB=8,则△AOB的面积为( )
如图,在半径为5的⊙O中,若弦AB=8,则△AOB的面积为( )| A、24 | B、16 | C、12 | D、8 |
 心为G.
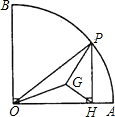
心为G. 如图,在半径为1的⊙O中,AB为直径,C为弧AB的中点,D为弧CB的三等分点,且弧DB的长等于弧CD长的两倍,连接AD并延长交⊙O的切线CE于点E(C为切点),则AE的长为
如图,在半径为1的⊙O中,AB为直径,C为弧AB的中点,D为弧CB的三等分点,且弧DB的长等于弧CD长的两倍,连接AD并延长交⊙O的切线CE于点E(C为切点),则AE的长为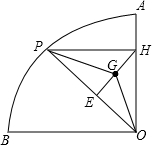
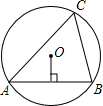 如图,在半径为2的⊙O中,圆心0到弦AB的距离为1,C为AB上方圆弧上任意一点,则∠ACB=
如图,在半径为2的⊙O中,圆心0到弦AB的距离为1,C为AB上方圆弧上任意一点,则∠ACB=