题目内容
 如图,∠BAC=∠ABC=45°,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.FE=1,BE=2.下列结论:①△CBE≌△ACD,②AD=6,③AF=BC,④BC=
如图,∠BAC=∠ABC=45°,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.FE=1,BE=2.下列结论:①△CBE≌△ACD,②AD=6,③AF=BC,④BC=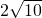 .其中正确的是
.其中正确的是
- A.①②③
- B.②③④
- C.①②④
- D.①③
C
分析:由AAS可证明△CBE≌△ACD,从而可判定①正确;
先证明△DFA∽△EFB,得出AD=2DF,又由①知AD=CE,设DF=x,则2x=x+3,解方程即可判定②正确;
如果AF=BC成立,那么由BC=AC,则AF=AC成立,∠ACF=∠AFC成立,根据等角的余角相等,得∠BCE=∠DAF成立,而∠BCE=∠CAD,即需∠CAD=∠DAF,但是已知条件没有交代,从而可判定③错误;
在直角△ACD中,由CD=2,AD=6,根据勾股定理即可判定④正确.
解答:∵∠BAC=∠ABC=45°,
∴CB=AC,∠ACB=90°.
在△CBE与△ACD中,
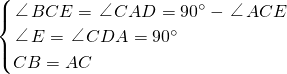 ,
,
∴△CBE≌△ACD,
故①正确;
∵BE⊥CE于E,AD⊥CE于D,
∴BE∥AD,
∴△DFA∽△EFB,
∴DF:EF=AD:BE,
∵FE=1,BE=2,
∴DF:1=AD:2,
∴AD=2DF.
设DF=x,则AD=2x.
 又由①知△CBE≌△ACD,
又由①知△CBE≌△ACD,
∴AD=CE,BE=CD=2,
∴2x=x+3,
∴x=3,
∴AD=2x=6,
故②正确;
假设AF=BC成立.
∵BC=AC,
∴AF=AC,
∴∠ACF=∠AFC,
∴∠BCE=∠DAF,
∵∠BCE=∠CAD,
∴∠CAD=∠DAF,
这与已知条件不符,
故③错误;
在直角△ACD中,∵∠ADC=90°,CD=2,AD=6,
∴AC= =2
=2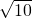 ,
,
故④正确.
故选C.
点评:本题主要考查了全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰直角三角形的判定与性质,综合性较强,难度中等.②中根据相似三角形的判定证明△DFA∽△EFB,并且根据其性质得出AD=2DF是解题的关键.
分析:由AAS可证明△CBE≌△ACD,从而可判定①正确;
先证明△DFA∽△EFB,得出AD=2DF,又由①知AD=CE,设DF=x,则2x=x+3,解方程即可判定②正确;
如果AF=BC成立,那么由BC=AC,则AF=AC成立,∠ACF=∠AFC成立,根据等角的余角相等,得∠BCE=∠DAF成立,而∠BCE=∠CAD,即需∠CAD=∠DAF,但是已知条件没有交代,从而可判定③错误;
在直角△ACD中,由CD=2,AD=6,根据勾股定理即可判定④正确.
解答:∵∠BAC=∠ABC=45°,
∴CB=AC,∠ACB=90°.
在△CBE与△ACD中,
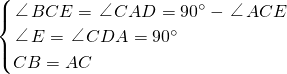 ,
,∴△CBE≌△ACD,
故①正确;
∵BE⊥CE于E,AD⊥CE于D,
∴BE∥AD,
∴△DFA∽△EFB,
∴DF:EF=AD:BE,
∵FE=1,BE=2,
∴DF:1=AD:2,
∴AD=2DF.
设DF=x,则AD=2x.
 又由①知△CBE≌△ACD,
又由①知△CBE≌△ACD,∴AD=CE,BE=CD=2,
∴2x=x+3,
∴x=3,
∴AD=2x=6,
故②正确;
假设AF=BC成立.
∵BC=AC,
∴AF=AC,
∴∠ACF=∠AFC,
∴∠BCE=∠DAF,
∵∠BCE=∠CAD,
∴∠CAD=∠DAF,
这与已知条件不符,
故③错误;
在直角△ACD中,∵∠ADC=90°,CD=2,AD=6,
∴AC=
 =2
=2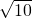 ,
,故④正确.
故选C.
点评:本题主要考查了全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰直角三角形的判定与性质,综合性较强,难度中等.②中根据相似三角形的判定证明△DFA∽△EFB,并且根据其性质得出AD=2DF是解题的关键.

练习册系列答案
相关题目
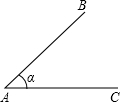 如图,∠BAC=45°,AB=4.现请你给定线段BC的长,使△ABC能构成等腰三角形.则BC的长可以是( )
如图,∠BAC=45°,AB=4.现请你给定线段BC的长,使△ABC能构成等腰三角形.则BC的长可以是( )| A、4 | ||
B、2
| ||
C、4或2
| ||
D、4或
|
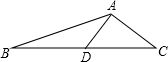 如图,∠BAC=120°,AD⊥AC,BD=CD,则下列结论正确的是( )
如图,∠BAC=120°,AD⊥AC,BD=CD,则下列结论正确的是( )| A、AD=AC | ||
B、AB=
| ||
| C、AB=2AC | ||
D、AB=
|
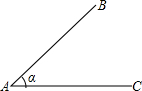 如图,∠BAC=45°,AB=6.现请你给定线段BC的长,使构成△ABC能构成等腰三角形.则BC的长可以是
如图,∠BAC=45°,AB=6.现请你给定线段BC的长,使构成△ABC能构成等腰三角形.则BC的长可以是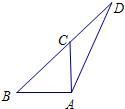
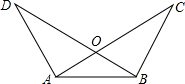 如图,∠BAC=∠ABD,BD、AC交于点O,要使OC=OD,还需添加一个条件,这个条件可以是
如图,∠BAC=∠ABD,BD、AC交于点O,要使OC=OD,还需添加一个条件,这个条件可以是