题目内容
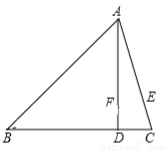
如图，∠BAC=45°，AB=6．现请你给定线段BC的长，使构成△ABC能构成等腰三角形．则BC的长可以是分析：没有指明等腰三角形的底边和腰，故应该分三种情况进行分析，从而不难求解．
解答：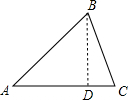
解：①当AB=AC时，
过点B作BD⊥AC
∵∠BAC=45°，AB=6
∴AD=BD=3
∵AB=AC=6
∴DC=6-3
∴BC=
=6
；
②当AB=BC时，
∵∠BAC=45°，AB=6，AB=BC
∴BC=6；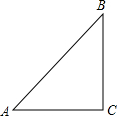
③当AC=BC时，
∵∠BAC=45°，AB=6，AC=BC
∴BC=3
故答案为：6
或6或3
．
解：①当AB=AC时，过点B作BD⊥AC
∵∠BAC=45°，AB=6
∴AD=BD=3
| 2 |
∵AB=AC=6
∴DC=6-3
| 2 |
∴BC=
| BD2+CD2 |
2-
|
②当AB=BC时，
∵∠BAC=45°，AB=6，AB=BC
∴BC=6；
③当AC=BC时，
∵∠BAC=45°，AB=6，AC=BC
∴BC=3
| 2 |
故答案为：6
2-
|
| 2 |
点评：此题主要考查等腰三角形的性质及勾股定理的综合运用．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
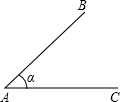如图，∠BAC=45°，AB=4．现请你给定线段BC的长，使△ABC能构成等腰三角形．则BC的长可以是（ ）| A、4 | ||
B、2
| ||
C、4或2
| ||
D、4或
|
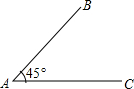如图，∠BAC=45°，AB=6，要使△ABC惟一确定，那么BC的长度x满足的条件是
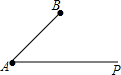如图，∠BAC=45°，AB=6，点C在射线AP上．现请你给定线段AC的长，使△ABC能构成等腰三角形．则AC的长可以是