题目内容
 如图,∠BAC=∠ABD,BD、AC交于点O,要使OC=OD,还需添加一个条件,这个条件可以是
如图,∠BAC=∠ABD,BD、AC交于点O,要使OC=OD,还需添加一个条件,这个条件可以是AC=BD
AC=BD
.分析:AC=BD,求出OA=OB,相减即可得出答案,此题答案不唯一,也可以∠D=∠C或∠DAB=∠CBA等.
解答:解:AC=BD,
理由是:∵∠BAC=∠ABD,
∴OB=OA,
∵AC=BD,
∴AC-OA=BD-OB,
∴OC=OD,
故答案为:AC=BD.
理由是:∵∠BAC=∠ABD,
∴OB=OA,
∵AC=BD,
∴AC-OA=BD-OB,
∴OC=OD,
故答案为:AC=BD.
点评:本题考查了全等三角形的性质和判定的应用,此题是一道开放性的题目,答案不唯一,培养了学生的发散思维能力.

练习册系列答案
相关题目
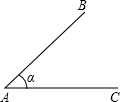 如图,∠BAC=45°,AB=4.现请你给定线段BC的长,使△ABC能构成等腰三角形.则BC的长可以是( )
如图,∠BAC=45°,AB=4.现请你给定线段BC的长,使△ABC能构成等腰三角形.则BC的长可以是( )| A、4 | ||
B、2
| ||
C、4或2
| ||
D、4或
|
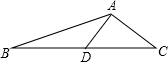 如图,∠BAC=120°,AD⊥AC,BD=CD,则下列结论正确的是( )
如图,∠BAC=120°,AD⊥AC,BD=CD,则下列结论正确的是( )| A、AD=AC | ||
B、AB=
| ||
| C、AB=2AC | ||
D、AB=
|
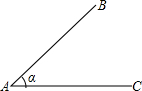 如图,∠BAC=45°,AB=6.现请你给定线段BC的长,使构成△ABC能构成等腰三角形.则BC的长可以是
如图,∠BAC=45°,AB=6.现请你给定线段BC的长,使构成△ABC能构成等腰三角形.则BC的长可以是