题目内容
【题目】如图,在△ABC 中,∠ABC=90°,AB=6,BC=8.点 M、N分别在边 AB、 BC上,沿直线 MN将△ABC折叠,点 B落在点 P处,如果 AP∥BC且 AP=4,那么 BN=________.
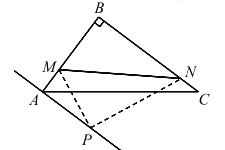
【答案】![]()
【解析】
证明∠MBO=∠BNO;求出BP、BO的长度;证明△ABP∽△OBN,列出比例式即可解决问题.
解:如图,连接BP,交MN于点O;
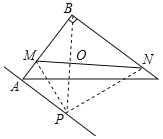
则BO=PO,BO⊥MN;
∵∠ABC=90°,
∴∠MBO+∠NBO=∠NBO+∠BNO,
∴∠MBO=∠BNO;
∵AP∥BC,且∠ABC=90°,
∴∠BAP=90°;
由勾股定理得:BP2=AB2+AP2,
∵AB=6,AP=4,
∴BP=![]() =2
=2![]() ,BO=
,BO=![]() ,
,
∵∠ABP=∠BNO,
∴△ABP∽△OBN,
∴![]() ,即
,即![]() ,
,
解得:BN=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目