题目内容
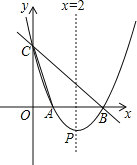
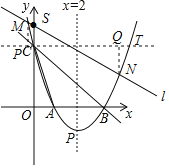
【题目】如图,直线y=﹣x+3与x轴,y轴分别相交于点B,C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求该抛物线的函数表达式;
(2)请问在抛物线上是否存在点Q,使得以点B,C,Q为顶点的三角形为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)过S(0,4)的动直线l交抛物线于M,N两点,试问抛物线上是否存在定点T,使得不过定点T的任意直线l都有∠MTN=90°?若存在,请求出点T的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣4x+3;(2)存在;(3)存在点T(4,3)使得不过定点T的任意直线l都有∠MTN=90°.
【解析】试题分析:(1)根据坐标轴上点的坐标特征可求,,再根据待定系数法可求抛物线的函数表达式;
(2)存在,分三种情况:过B点垂直BC的直线的解析式为y=x+b,过C点垂直BC的直线解析式为y=x+3,以BC为斜边,进行讨论可求点Q的坐标;
(3)设M(x1,y1), N(x2,y2), T(a,b),过T作PQ∥x轴,过M,N作MP⊥PQ于P,NQ⊥PQ于Q,可证△MPT∽TQN,根据相似三角形的性质求解.
解:(1)∵直线y=﹣x+3与x轴,y轴分别相交于点B,C,
∴B(3,0),C(0,3),
∵对称轴为直线x=2,
∴设该抛物线的函数表达式为y=a(x﹣1)(x﹣3),
把C(0,3)代入得3a=3,解得a=1,
∴该抛物线的函数表达式y=(x﹣1)(x﹣3)=x2﹣4x+3;
(2)存在,设过B点垂直BC的直线的解析式为y=x+b,
把B(3,0)代入得b=﹣3,
则直线的解析式为y=x﹣3,
依题意有![]() ,
,
解得![]() ,
,![]() ,
,
∴Q1(2,﹣1),
过C点垂直BC的直线解析式为y=x+3,
依题意有![]() ,
,
解得![]() ,
,![]() ,
,
∴Q2(5,8),
以BC为斜边,设β(a,a2﹣4a+3),则
a2+(a2﹣4a)2+(a﹣3)2+(a2﹣4a+3)2=18,
a3﹣8a2+20a﹣15=0,
(a﹣3)(a2﹣5a+5)=0,
解得a1=3,a2=![]() ,
,
∴Q3(![]() ,
,![]() ),Q4(
),Q4(![]() ,
,![]() ),
),
∴存在点Q,使得以点B,C,Q为顶点的三角形为直角三角形;
(3)设M(x1,y1),N(x2,y2),T(a,b),
过T作PQ∥x轴,过M,N作MP⊥PQ于P,NQ⊥PQ于Q,则∠MTN=90°,
则△MPT∽△TQN,
∴![]() ,
,
a(x1+x2)﹣a2﹣x1x2=y1y2﹣b(y1+y2)+b2,
其中x1,x2,y1,y2是![]() 的解,
的解,
∴x2﹣(4+k)x﹣1=0,
x1x2=﹣1,
x1+x2=k+4,
y1y2=k2x1x2+4k(x1+x2)+16=﹣k2+4k(k+4)+16,
y1+y2=k(k+4)+8,
1+a(k+4)﹣a2=﹣k2+4k(k+4)+16﹣b(k2+4k+8)+b2,
1+ak+4a﹣a2=﹣k3+4k2+16k+16﹣bk2﹣4bk﹣8b+b2,
∴(3﹣b)k2+(16﹣4b﹣a)k+a2﹣4a﹣8b+b2+15=0,
∵y=kx+b有无数条,
∴k为任何实数,3﹣b=0,16﹣4b﹣a=0,a2﹣4a﹣8b+b2+15=0,
解得a=4,b=3,
存在点T(4,3)使得不过定点T的任意直线l都有∠MTN=90°.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案