题目内容
【题目】菱形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上.
上.
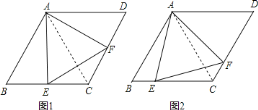
(1)如图![]() ,若
,若![]() 是
是![]() 的中点,
的中点,![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,若
,若![]() ,求证:
,求证:![]() 是等边三角形.
是等边三角形.

【答案】见解析
【解析】
(1)首先连接AC,由菱形ABCD中,∠B=60°,根据菱形的性质,易得△ABC是等边三角形,又由三线合一,可证得AE⊥BC,继而求得∠FEC=∠CFE,即可得EC=CF,继而证得BE=DF;
(2)首先由△ABC是等边三角形,即可得AB=AC,以求得∠ACF=∠B=60°,然后利用平行线与三角形外角的性质,可求得∠AEB=∠AFC,证得△AEB≌△AFC,即可得AE=AF,证得:△AEF是等边三角形.
解:(1)连接![]() ,
,
∵在菱形![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
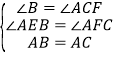
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形.
是等边三角形.

练习册系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A. 1 B. 2 C. 3 D. 4