题目内容
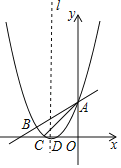
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,顶点A、C分别在x轴、y轴上,反比例函数y=![]() (k≠0,x>0)的图象与正方形OABC的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN,则下列选项中的结论错误的是( )
(k≠0,x>0)的图象与正方形OABC的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN,则下列选项中的结论错误的是( )
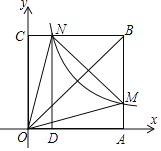
A. △ONC≌△OAM
B. 四边形DAMN与△OMN面积相等
C. ON=MN
D. 若∠MON=45°,MN=2,则点C的坐标为(0,![]() +1)
+1)
【答案】C
【解析】根据反比例函数的比例系数的几何意义得到S△ONC=S△OAM=![]() k,即
k,即![]() OCNC=
OCNC=![]() OAAM,而OC=OA,则NC=AM,再根据“SAS”可判断△OCN≌△OAM;根据S△OND=S△OAM=
OAAM,而OC=OA,则NC=AM,再根据“SAS”可判断△OCN≌△OAM;根据S△OND=S△OAM=![]() k和S△OND+S四边形DAMN=S△OAM+S△OMN,即可得到S四边形DAMN=S△OMN;
k和S△OND+S四边形DAMN=S△OAM+S△OMN,即可得到S四边形DAMN=S△OMN;
根据全等的性质得到ON=OM,由于k的值不能确定,则∠MON的值不能确定,无法确定△ONM为等边三角形,则ON≠MN;作NE⊥OM于E点,则△ONE为等腰直角三角形,设NE=x,则OM=ON=x,EM=![]() x-x=(
x-x=(![]() -1)x,在Rt△NEM中,利用勾股定理可求出x2=2+
-1)x,在Rt△NEM中,利用勾股定理可求出x2=2+![]() ,所以ON2=(
,所以ON2=(![]() x)2=4+2
x)2=4+2![]() ,易得△BMN为等腰直角三角形,得到BN=
,易得△BMN为等腰直角三角形,得到BN=![]() MN=
MN=![]() ,设正方形ABCO的边长为a,在Rt△OCN中,利用勾股定理可求出a的值为
,设正方形ABCO的边长为a,在Rt△OCN中,利用勾股定理可求出a的值为![]() +1,从而得到C点坐标为(0,
+1,从而得到C点坐标为(0,![]() +1).
+1).
∵点M、N都在y=![]() 的图象上,
的图象上,
∴S△ONC=S△OAM=![]() k,即
k,即![]() OCNC=
OCNC=![]() OAAM,
OAAM,
∵四边形ABCO为正方形,
∴OC=OA,∠OCN=∠OAM=90°,
∴NC=AM,
∴△OCN≌△OAM,
∴A正确;
∵S△OND=S△OAM=![]() k,
k,
而S△OND+S四边形DAMN=S△OAM+S△OMN,
∴四边形DAMN与△MON面积相等,
∴B正确;
∵△OCN≌△OAM,
∴ON=OM,
∵k的值不能确定,
∴∠MON的值不能确定,
∴△ONM只能为等腰三角形,不能确定为等边三角形,
∴ON≠MN,
∴C错误;
作NE⊥OM于E点,如图所示:
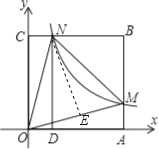
∵∠MON=45°,∴△ONE为等腰直角三角形,
∴NE=OE,
设NE=x,则ON=![]() x,
x,
∴OM=![]() x,
x,
∴EM=![]() x-x=(
x-x=( ![]() -1)x,
-1)x,
在Rt△NEM中,MN=2,
∵MN2=NE2+EM2,即22=x2+[( ![]() -1)x]2,
-1)x]2,
∴x2=2+![]() ,
,
∴ON2=(![]() x)2=4+2
x)2=4+2![]() ,
,
∵CN=AM,CB=AB,
∴BN=BM,
∴△BMN为等腰直角三角形,
∴BN=![]() MN=
MN=![]() ,
,
设正方形ABCO的边长为a,则OC=a,CN=a-![]() ,
,
在Rt△OCN中,∵OC2+CN2=ON2,
∴a2+(a-![]() )2=4+2
)2=4+2![]() ,解得a1=
,解得a1=![]() +1,a2=-1(舍去),
+1,a2=-1(舍去),
∴OC=![]() +1,
+1,
∴C点坐标为(0,![]() +1),
+1),
∴D正确.
故选:C.

 智慧小复习系列答案
智慧小复习系列答案