题目内容
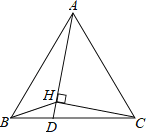
【题目】如图,在△ABC中AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求
(1)∠BAE的度数.
(2)∠DAE的度数.
(3)探究:有的同学认为无论∠B、∠C的度数是多少,都有∠DAE=![]()
![]() (∠B-∠C)成立,你同意吗?并说出成立或不成立的理由.
(∠B-∠C)成立,你同意吗?并说出成立或不成立的理由.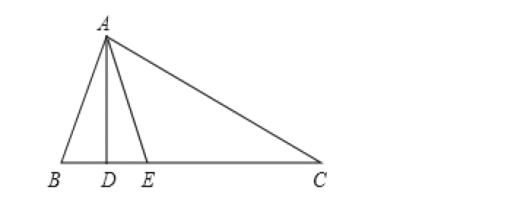
【答案】(1)40°;(2)20°;(3)成立,理由见解析.
【解析】
(1)先根据三角形内角和定理求出∠BAC,再根据角平分线求出即可;(2)根据AD⊥BC和三角形内角和定理求出∠BAD,再根据(1)中∠BAE的度数,求出即可;(3)先根据三角形内角和定理及角平分线用∠B、∠C表示出∠BAE,再根据垂直,用∠B表示出∠BAD,化简即可.
(1)∵在△ABC中,∠B=70°,∠C=30°,
∴∠BAC=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() ×80°=40°;
×80°=40°;
(2)∵AD⊥BC,∠B=70°,
∴∠BAD=90°-∠B=90°-70°=20°,
∴∠DAE=∠BAE-∠BAD=40°-20°=20°;
(3)成立,理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() (180°-∠B-∠C),
(180°-∠B-∠C),
∵AD⊥BC,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=![]() (180°-∠B-∠C)-(90°-∠B)=
(180°-∠B-∠C)-(90°-∠B)=![]() (∠B-∠C),
(∠B-∠C),
则成立.

【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人.行驶路程记录如下(规定向南为正,向北为负,单位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
5 | 2 | -4 | -3 | 10 |
(1)接送完第5批客人后,该驾驶员在公司 边(填南或北),距离公司 千米.
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油 升.
(3)若该出租车的计价标准为:行驶路程不超过3![]() 收费10元,超过3
收费10元,超过3![]() 的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?
的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?
【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?