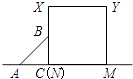题目内容
【题目】现用![]() 根长度相同的火柴棒,按如图①摆放时可摆成
根长度相同的火柴棒,按如图①摆放时可摆成![]() 个正方形,按如图②摆放时可摆成
个正方形,按如图②摆放时可摆成![]() 个正方形
个正方形
(1)如图①,当![]() 时,
时,![]() ___________,如图②,当
___________,如图②,当![]() 时,
时,![]() ________________;
________________;
(2)![]() 与
与![]() 之间有何数量关系,请你写出来并说明理由;
之间有何数量关系,请你写出来并说明理由;
(3)现有61根火柴棒,现用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状。请你直接写出一种摆放方法,并通过计算验证你的结论


【答案】(1)①10;②12;(2)3m=5n+1;(3)见解析
【解析】
(1)根据每多一个正方形多用2根火柴棒写出摆放m个正方形所用的火柴棒的根数,然后把m=3代入进行计算即可得解;根据每多2个正方形多用5根火柴棒写出摆放2n个小正方形所用的火柴棒的根数,然后把m=2代入,进行计算即可得解;(2)根据a相等列出关于m、n的关系式;(3)可以摆出图①说明a是比3的倍数多1的数,可以摆出图②说明2a是比5的倍数多2的数,所以,2a取5与6的倍数大2的数,并且现有61根火柴棒进而得出答案.
解:(1)由图可知,图①每多1个正方形,多用3根火柴棒,所以,m个小正方形共用3m+1根火柴棒,
图②每多2个正方形,多用5根火柴棒,所以,2n个小正方形共用5n+2根火柴棒,
当m=3时,a=3×3+1=10,
图②可以摆放2×5=12个小正方形;
故答案为:10,12;
(2)∵都用a根火柴棒,
∴3m+1=5n+2,
整理得,3m=5n+1;
(3)∵3m+1+5n+2=61,
∴3m+5n=58,
当m=1,n=11,是方程的根,
∴第一个图形摆放3×1+1=4根火柴棒,
第二个图形摆放5×11+2=57根火柴棒,
∵4+57=61,
∴符合题意(答案不唯一).

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?