题目内容
 一次函数的图象经过A(-3,10)和B(-1,6).
一次函数的图象经过A(-3,10)和B(-1,6).(1)求这个函数的解析式,并画出函数的图象;
(2)求这个函数的图象与两坐标轴围成的三角形面积.
分析:(1)利用待定系数法求解析式并利用图象与坐标轴的交点坐标画出直线;
(2)先求函数y=-2x+4与两坐标轴的交点分别为(0,4),(2,0),从而求的直线与两坐标轴围成的三角形面积为4.
(2)先求函数y=-2x+4与两坐标轴的交点分别为(0,4),(2,0),从而求的直线与两坐标轴围成的三角形面积为4.
解答: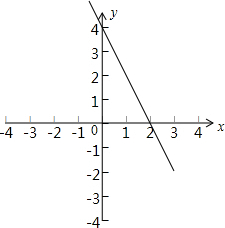 解:(1)设这个函数为y=kx+b
解:(1)设这个函数为y=kx+b
由条件得
,
解之得:
,
所以这个函数为y=-2x+4.
(2)函数y=-2x+4与两坐标轴的交点分别为(0,4),(2,0),
∴直线与两坐标轴围成的三角形面积为
×2×4=4.
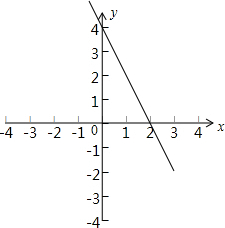 解:(1)设这个函数为y=kx+b
解:(1)设这个函数为y=kx+b由条件得
|
解之得:
|
所以这个函数为y=-2x+4.
(2)函数y=-2x+4与两坐标轴的交点分别为(0,4),(2,0),
∴直线与两坐标轴围成的三角形面积为
| 1 |
| 2 |
点评:主要考查了用待定系数法解函数解析式和一次函数图象的性质,要掌握函数解析式的意义,尤其是与坐标轴的交点.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
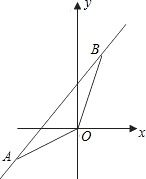 如图,已知一次函数的图象经过A(-2,-1),B(1,3)两点.
如图,已知一次函数的图象经过A(-2,-1),B(1,3)两点. 已知一次函数的图象经过(2,5)和(-1,-1)两点.
已知一次函数的图象经过(2,5)和(-1,-1)两点. 26、已知一次函数的图象经过点A(-3,0),B(-1,1)两点.
26、已知一次函数的图象经过点A(-3,0),B(-1,1)两点.