题目内容
规定1！=1×1，2！=2×1，3！=3×2×，…已知a！=5040，那么a=（ ）
分析：1！=1×1，2！=2×1，3！=3×2×1，…可知：
a！=a×（a-1）×（a-2）×（a-3）×…×2×1；
a！=5040，求a就是求1×2×3×4×…×a=5040；逐步计算，看乘到哪个数积是5040即可．
a！=a×（a-1）×（a-2）×（a-3）×…×2×1；
a！=5040，求a就是求1×2×3×4×…×a=5040；逐步计算，看乘到哪个数积是5040即可．
解答：解：a！=5040，即1×2×3×4×…×a=5040；
因为1×2×3×4×5×6×7=5040；
所以a=7；
故选：C．
因为1×2×3×4×5×6×7=5040；
所以a=7；
故选：C．
点评：本题理解a！的计算方法，然后由此逐数相乘求解．
练习册系列答案
名校通行证有效作业系列答案
相关题目
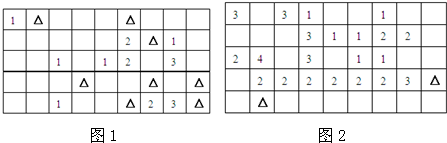
如图，圆周上顺次排列着1、2、3、…、12这十二个数，我们规定：相邻的四个数a1、a2、a3、a4顺序颠倒为a4、a3、a2、a1，称为一次“变换”（如：1、2、3、4变为4、3、2、1，又如：11、12、1、2变为2、1、12、11）．能否经过有限次“变换”，将十二个数的顺序变为9、1、2、3、…8、10、11、12（如图）？请说明理由．