题目内容
有7个各不相同的正整数,它们的平均数是100.把它们按从小到大排列,前3个数的平均数是20,后三个数的平均数是200.最小的数最大是 ,最大的数最大是 .
分析:中间的数是:100×7-20×3-200×3=40,所以前三个数最大小于40,后三个数的最小要大于40,要使前3个数中最小的数最大,那么这三个数要相差1,所以最小的数最大是:20-1=19;同理,要使最大的数最大,那么后三个数中的前两个要最小,而且也相差1,即第一个数是40+1=41,第二个数是41+1=42,因此最大的数最大是:200×3-41-42=517;据此解答.
解答:解:中间的数是:100×7-20×3-200×3=40,
所以前三个数最大小于40,后三个数的最小要大于40,
前3个数:最小的数最大是:20-1=19;
同理,后三个数中第一个数是40+1=41,第二个数是41+1=42,
因此最大的数最大是:200×3-41-42=517;
答:最小的数最大是19,最大的数最大是517.
故答案为:19,517.
所以前三个数最大小于40,后三个数的最小要大于40,
前3个数:最小的数最大是:20-1=19;
同理,后三个数中第一个数是40+1=41,第二个数是41+1=42,
因此最大的数最大是:200×3-41-42=517;
答:最小的数最大是19,最大的数最大是517.
故答案为:19,517.
点评:本题考查的知识点比较多,有平均数求法的灵活逆用,极值的确定,整数的拆分,关键是明确:和一定,几个数的差越小,就这几个数越接近;差越大,这几个数就会走向两个极端.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
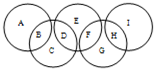 如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,且每个圆中所填数的和都等于2008.这九个数总和最小为
如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,且每个圆中所填数的和都等于2008.这九个数总和最小为