题目内容
 如图,四边形EFGH的面积是66平方米.EA=AB,CB=BF,DC=CG,HD=DA.求四边形ABCD的面积.
如图,四边形EFGH的面积是66平方米.EA=AB,CB=BF,DC=CG,HD=DA.求四边形ABCD的面积.分析:根据四边形ABCD的面积是66平方米,要求四边形ABCD的面积,只要求出四边形ABCD与四周多出来的四个三角形的面积的关系以及四边形ABCD与四边形EFGH的面积关系,即可解决问题.


解答:解:连接CA、AF、HC,则三角形ADC的面积=三角形HDC的面积=三角形HCG的面积=
三角形HDG的面积
同理,三角形ABC的面积=三角形ABF的面积=三角形AEF的面积=
三角形BEF的面积
同理,如果连接BD,可以得到三角形ABD=
三角形AEH的面积和三角形BCD=
三角形CFG的面积
则四个式子相加得四边形ABCD的面积的2倍=
(EFGH-ABCD)的面积,据此解得ABCD的面积为13.2平方米
答:四边形ABCD的面积是13.2平方米.
| 1 |
| 2 |
同理,三角形ABC的面积=三角形ABF的面积=三角形AEF的面积=
| 1 |
| 2 |
同理,如果连接BD,可以得到三角形ABD=
| 1 |
| 2 |
| 1 |
| 2 |
则四个式子相加得四边形ABCD的面积的2倍=
| 1 |
| 2 |
答:四边形ABCD的面积是13.2平方米.
点评:解答此题的关键是,根据题意,添加辅助线,利用三角形的面积公式,帮助我们找到三角形之间的关系,由此即可解答.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图,四边形ABCD和EFGH都是正方形,且边长均为2cm.又E点是正方形 ABCD的中心,求两个正方形公共部分(图中阴影部分)的面积S.
如图,四边形ABCD和EFGH都是正方形,且边长均为2cm.又E点是正方形 ABCD的中心,求两个正方形公共部分(图中阴影部分)的面积S. 如图,四边形ABCD和EFGH都是平行四边形,四边形ABCD的面积是16,BG:GC=3:1,则四边形EFGH的面积=
如图,四边形ABCD和EFGH都是平行四边形,四边形ABCD的面积是16,BG:GC=3:1,则四边形EFGH的面积=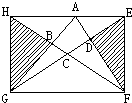 如图,长方形EFGH的长HE和宽EF分别是6cm和4cm,四边形ABCD的面积为1.8平方厘米,那么阴影部分的面积和为多少平方厘米?
如图,长方形EFGH的长HE和宽EF分别是6cm和4cm,四边形ABCD的面积为1.8平方厘米,那么阴影部分的面积和为多少平方厘米?