题目内容
 如图,四边形ABCD和EFGH都是平行四边形,四边形ABCD的面积是16,BG:GC=3:1,则四边形EFGH的面积=
如图,四边形ABCD和EFGH都是平行四边形,四边形ABCD的面积是16,BG:GC=3:1,则四边形EFGH的面积=3
3
.分析:①由BG:GC=3:1,可得出GC=
BC,平行四边形AGCE和ABCD同高,底是ABCD的
,所以面积也是其
,即平行四边形AGCE=16×
=4;
②平行四边形EFGH和平行四边形AGCE同高,底是平行四边形AGCE的
,所以面积也是其
,即平行四边形EFGH的面积=4×
=3.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
②平行四边形EFGH和平行四边形AGCE同高,底是平行四边形AGCE的
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:根据题干分析可得:
平行四边形AGCE的面积=16×
=4;
平行四边形EFGH的面积=4×
=3.
答:平行四边形EFGH的面积为:3.
故答案为:3.
平行四边形AGCE的面积=16×
| 1 |
| 4 |
平行四边形EFGH的面积=4×
| 3 |
| 4 |
答:平行四边形EFGH的面积为:3.
故答案为:3.
点评:此题根据平行四边形的底与高的关系,推理得出要求的平行四边形EFGH的面积与已知平行四边形的面积的倍数关系,然后进行计算即可解决.

练习册系列答案
相关题目
 如图平行四边形ABCD的面积是36平方厘米,其中AE=
如图平行四边形ABCD的面积是36平方厘米,其中AE= 如图,四边形ABCD内有一点O,且O点到四条边AB、BC、CD、AD的距离都等于8厘米.若四边形ABCD的周长是62厘米.那么,四边形ABCD的面积是
如图,四边形ABCD内有一点O,且O点到四条边AB、BC、CD、AD的距离都等于8厘米.若四边形ABCD的周长是62厘米.那么,四边形ABCD的面积是 如图,四边形ABCD的周长是60厘米,点M到各边的距离都是4.5厘米,这个四边形的面积是
如图,四边形ABCD的周长是60厘米,点M到各边的距离都是4.5厘米,这个四边形的面积是 如图,四边形ABCD是边长为8厘米的正方形,三角形ADF的面积比三角形CEF
如图,四边形ABCD是边长为8厘米的正方形,三角形ADF的面积比三角形CEF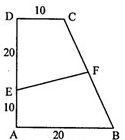 如图,四边形ABCD是直角梯形,∠A=∠D=90?,点E将DA分成2:1,F为BC中点,则四边形FEAB的面积为
如图,四边形ABCD是直角梯形,∠A=∠D=90?,点E将DA分成2:1,F为BC中点,则四边形FEAB的面积为