题目内容
 如图,c=6,三个同心圆的半径依次为
如图,c=6,三个同心圆的半径依次为| c-2 |
| 4 |
| c+2 |
| 4 |
| c |
| 2 |
5:36
5:36
.分析:当c=6时,
=1,
=2,
=3,结合图形发现:阴影部分可以分为三部分进行计算,一是半径为1的最小圆内圆心角为90°的扇形面积;二是内圆半径为1,外圆半径为2,圆心角为20°的圆环的面积,三是内圆半径为2,外圆半径为3,圆心角为60°的圆环的面积,由此利用扇形和圆环的面积公式即可求出阴影部分的面积,再利用圆的面积公式求出最大圆的面积即可求出它们的面积之比.
| c-2 |
| 4 |
| c+2 |
| 4 |
| c |
| 2 |
解答:解:当c=6时,
=1,
=2,和
=3,
阴影部分的面积是:
π×12+
π(22-12)+
π(32-22),
=
π+
π×(4-1)+
π×(9-4),
=
π+
π+
π,
=
π;
大圆的面积是:π×32=9π,
则它们的面积之比是:
π:9π=5:36,
答:它们的面积之比是5:36,
故答案为:5:36.
| c-2 |
| 4 |
| c+2 |
| 4 |
| c |
| 2 |
阴影部分的面积是:
| 90 |
| 360 |
| 20 |
| 360 |
| 60 |
| 360 |
=
| 1 |
| 4 |
| 1 |
| 18 |
| 1 |
| 6 |
=
| 1 |
| 4 |
| 1 |
| 6 |
| 5 |
| 6 |
=
| 5 |
| 4 |
大圆的面积是:π×32=9π,
则它们的面积之比是:
| 5 |
| 4 |
答:它们的面积之比是5:36,
故答案为:5:36.
点评:此题考查了扇形与圆环的面积公式的灵活应用,此题计算较为复杂,要求学生熟记公式进行计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,c=6,三个同心圆的半径依次为
如图,c=6,三个同心圆的半径依次为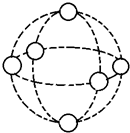 如图,球体上有三个圆,在六个○里分别填上1、2、3、4、5、6,使得每圆周上四个数的和都相等,都是
如图,球体上有三个圆,在六个○里分别填上1、2、3、4、5、6,使得每圆周上四个数的和都相等,都是 如图,c=6,三个同心圆的半径依次为
如图,c=6,三个同心圆的半径依次为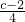 ,
, ,和
,和 ,图中阴影部分的面积与最大圆面积的比是________.
,图中阴影部分的面积与最大圆面积的比是________. ,
, ,和
,和 ,图中阴影部分的面积与最大圆面积的比是( )。
,图中阴影部分的面积与最大圆面积的比是( )。