题目内容
甲、乙分别从A、C两地同时出发,匀速相向而行,他们的速度比是5:3,相遇于B地后,甲继续以原来的速度前进,而乙立刻掉头返回,并且乙的速度比原来降低
,这样当乙回到C地时,而甲刚好到达离C地32千米的D处,那么A、C两地之间的距离是多少千米?
| 2 |
| 5 |
考点:相遇问题
专题:综合行程问题
分析:如图:设A、C两地之间的距离是x千米;因为甲、乙速度比是5:3,可设甲的速度是5v,乙的速度是3v;
则A、B两地之间的距离是
x,B、C两地之间的距离是
x;根据乙掉头从B返回C的时间等于甲从B到D的时间,列出方程解答求出x即可.
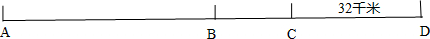
则A、B两地之间的距离是
| 5 |
| 8 |
| 3 |
| 8 |
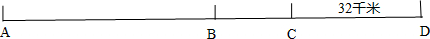
解答:
解:设A、C两地之间的距离是x千米;因为甲、乙速度比是5:3,可设甲的速度是5v,乙的速度是3v;
根据题意得:
=
v(
x+32)=
vx
(
x+32)=
x
x=48
答:A、C两地之间的距离是48千米.
根据题意得:
| ||
| 5v |
| ||
3v(1-
|
| 9 |
| 5 |
| 3 |
| 8 |
| 15 |
| 8 |
| 9 |
| 5 |
| 3 |
| 8 |
| 15 |
| 8 |
x=48
答:A、C两地之间的距离是48千米.
点评:解答本题的关键是能根据乙掉头从B返回C的时间等于甲从B到D的时间列出方程.

练习册系列答案
相关题目
 某触屏智能手机屏幕尺寸为80mm×50mm,原来的主屏幕放置5行×4列共20枚大小一致的正方形图标,边长为8mm.系统升级后,上面的16个正方形图标变成圆角方形图标,其四个圆角是半径为1mm的四分之一圆,下面的四个正方形图标变成半径为4mm的3个圆形图标.则新系统下屏幕除去图标以外剩余部分的面积是多少?(π取3.14)
某触屏智能手机屏幕尺寸为80mm×50mm,原来的主屏幕放置5行×4列共20枚大小一致的正方形图标,边长为8mm.系统升级后,上面的16个正方形图标变成圆角方形图标,其四个圆角是半径为1mm的四分之一圆,下面的四个正方形图标变成半径为4mm的3个圆形图标.则新系统下屏幕除去图标以外剩余部分的面积是多少?(π取3.14)
