Question

18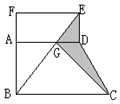．如图，是长方形ADEF和直角梯形ABCD组成的组合图形，已知长方形AFED的面积是90平方厘米，求阴影部分面积．

Answer 1

分析 利用等积变换思想，将所求阴影部分面积转化成一个规则的易求的几何图形的面积．首先，△GCD的面积等于△GDB的面积，而△BCE的面积等于△DEF的面积．

解答 解：如图，连接BD．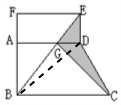


因为AD∥BC
所以S_△GCD=S_△GDB
因为FE∥AD，
所以S_△BCE=S_△DEF=$\frac{1}{2}$×90=45（平方厘米）
即阴影部分的面积为45平方厘米．
答：阴影部分面积是45平方厘米．

点评 本题主要考查了三角形面积的等积变换，难度不大，但却是一道经典好题．巧妙地将所求阴影部分的面积转化成△EFD的面积是解决本题的关键．