题目内容
已知一个四位数平方之后,后四位与原来的四位数相同,那么原来那个四位数是 .
考点:完全平方数性质
专题:计算问题(巧算速算)
分析:设原来四位数是abcd=1000a+100b+10c+d,则(1000a+100b+10c+d)×(1000a+100b+10c+d)=106?a2+10000b2+200000ab+20000ac+2000(ad+bc)+100×(c2+2bd)+20cd+d2,所以一个四位数平方之后的后四位数与2000(ad+bc)+100×(c2+2bd)+20cd+d2的后四位数相同,推理,可得a=9,b=3,c=7,d=6,进而求出原来的四位数是多少即可.
解答:
解:设原来四位数是abcd=1000a+100b+10c+d,
则(1000a+100b+10c+d)×(1000a+100b+10c+d)
=106?a2+10000b2+200000ab+20000ac+2000(ad+bc)+100×(c2+2bd)+20cd+d2,
所以一个四位数平方之后的后四位数与2000(ad+bc)+100×(c2+2bd)+20cd+d2的后四位数相同,
推理,可得a=9,b=3,c=7,d=6,
即原来的四位数是9376,93762=87909376.
故答案为:9376.
则(1000a+100b+10c+d)×(1000a+100b+10c+d)
=106?a2+10000b2+200000ab+20000ac+2000(ad+bc)+100×(c2+2bd)+20cd+d2,
所以一个四位数平方之后的后四位数与2000(ad+bc)+100×(c2+2bd)+20cd+d2的后四位数相同,
推理,可得a=9,b=3,c=7,d=6,
即原来的四位数是9376,93762=87909376.
故答案为:9376.
点评:此题主要考查了完全平方数性质的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
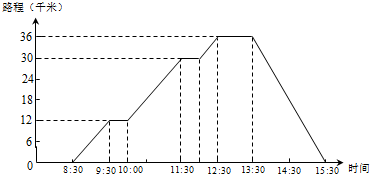 周末李艳和朋友从家出发骑车到红格去玩,请根据统计图回答问题.
周末李艳和朋友从家出发骑车到红格去玩,请根据统计图回答问题.