题目内容
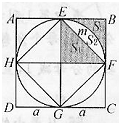 如图,边长为2a的正方形ABCD内有一个最大的圆圆O,圆O内有一个最大的正方形EFGH.用S1,S2,S3依次表示△EOF的面积,弓形EmF的面积,带弧边EmF的△EBF的面积,则S1*S2*S3=
如图,边长为2a的正方形ABCD内有一个最大的圆圆O,圆O内有一个最大的正方形EFGH.用S1,S2,S3依次表示△EOF的面积,弓形EmF的面积,带弧边EmF的△EBF的面积,则S1*S2*S3=a6÷32
a6÷32
.(圆周率π取3)分析:根据题意,S1的面积可用三角形的面积公式进行计算;S2的面积等于正方形ABCD内最大圆面积的四分之一,即
圆的面积;S3的面积等于
正方形ABCD的面积减去S1与S2的面积之和,最后再把S1,S2,S3的面积相乘即可.
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:S1=a2÷2;
S2=(a2π)÷4-(a2÷2),
=a2÷2×(
-1),
=a2÷4;
S3=a2-(a2π)÷4,
=a2×(1-
),
=a2÷4;
S1×S2×S3
=(a2÷2)×(a2÷4)×(a2÷4),
=a6÷32.
故答案为:a6÷32.
S2=(a2π)÷4-(a2÷2),
=a2÷2×(
| π |
| 2 |
=a2÷4;
S3=a2-(a2π)÷4,
=a2×(1-
| π |
| 4 |
=a2÷4;
S1×S2×S3
=(a2÷2)×(a2÷4)×(a2÷4),
=a6÷32.
故答案为:a6÷32.
点评:此题主要考查的是圆的面积公式、三角形面积公式和正方形面积公式的综合应用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图,边长为12cm的正方形与直径为16cm的圆部分重叠(圆心是正方形的一个顶点),用S1,S2分别表示两块空白部分的面积,则S1-S2=
如图,边长为12cm的正方形与直径为16cm的圆部分重叠(圆心是正方形的一个顶点),用S1,S2分别表示两块空白部分的面积,则S1-S2= 如图是边长为1的正方形和一个梯形拼成的“火炬“.梯形的上底长1.5米,A为上底的中点,B为下底的中点,线段AB恰好是梯形的高,长为0.5米,CD长为
如图是边长为1的正方形和一个梯形拼成的“火炬“.梯形的上底长1.5米,A为上底的中点,B为下底的中点,线段AB恰好是梯形的高,长为0.5米,CD长为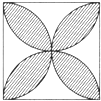 如图,边长为4cm的正方形,分别以四条边为直径向正方形内作半圆,求图中阴影部分面积.
如图,边长为4cm的正方形,分别以四条边为直径向正方形内作半圆,求图中阴影部分面积. 如图,边长为2a的正方形ABCD内有一个最大的圆圆O,圆O内有一个最大的正方形EFGH.用S1,S2,S3依次表示△EOF的面积,弓形EmF的面积,带弧边EmF的△EBF的面积,则S1*S2*S3=________.(圆周率π取3)
如图,边长为2a的正方形ABCD内有一个最大的圆圆O,圆O内有一个最大的正方形EFGH.用S1,S2,S3依次表示△EOF的面积,弓形EmF的面积,带弧边EmF的△EBF的面积,则S1*S2*S3=________.(圆周率π取3)