题目内容
如图，边长为12cm的正方形与直径为16cm的圆部分重叠（圆心是正方形的一个顶点），用S1，S2分别表示两块空白部分的面积，则S1-S2=48
48
cm2（圆周率π取3）．分析：根据图意可得：S1-S2=（S1+S阴）-（S2+S阴）=S圆-S正=3×（16÷2）2-122=192-144=48（平方厘米）；据此解答．
解答：解：3×（16÷2）2-122
=192-144，
=48（平方厘米）；
答：S1-S2=48cm2．
故答案为：48．
=192-144，
=48（平方厘米）；
答：S1-S2=48cm2．
故答案为：48．
点评：本题考查了差不变面积问题和重叠问题的灵活应用，重点是明确把重叠部分从整体上去考虑．
练习册系列答案
相关题目
（2009?大竹县）如图，正方形ABCD中，边长为12cm，CE=2BE，AF=2BF，AE、CF交于点O，求阴影部分的面积．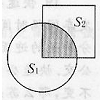
如图，边长12cm的正方形与直径为16cm的圆部分重叠，若没有重叠的两空白部分的面积分别是S1，S2，则S1-S2=
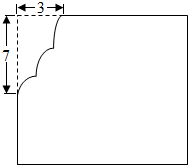将一块边长为12cm的有缺损的正方形铁皮（如图）剪成一块无缺损的正方形铁皮，则剪成的正方形铁皮的面积的最大值是（ ） 
连接立方体各面的中心构成一个正八面体（如图所示）．已知立方体的边长为12cm，请问正八面体之体积是多少