题目内容
17.某次捐款活动中甲班20人,每人捐款10元,乙班30人,每人捐款数比甲、乙两班平均每人捐款数多2元,两个班共捐款多少元?分析 设乙班每人捐款x元,根据乙班每人捐款数比甲、乙两班平均每人捐款数多2元,可列出方程x-(10×20+30x)÷(20+30)=2,依据等式的性质求出x的值,再根据总价=单价×数量,分别求出甲班、乙班各捐款多少钱,再相加即可.
解答 解:设乙班每人捐款x元,
x-(10×20+30x)÷(20+30)=2
x-(200+30x)÷50=2
x-4-$\frac{3}{5}$x=2
$\frac{2}{5}$x-4=2
$\frac{2}{5}$x-4+4=2+4
$\frac{2}{5}$x=6
$\frac{2}{5}$x÷$\frac{2}{5}$x=6÷$\frac{2}{5}$
x=15;
10×20+15×30
=200+450
=650(元);
答:两个班共捐款650元.
点评 解答此题关键是根据乙班每人捐款数比甲、乙两班平均每人捐款数多2元,列出方程求出乙班每人捐款多少元数,再进一步解答即可.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
8.一个数的分子扩大2倍,分母也扩大2倍,这个分数的大小( )
| A. | 不变 | B. | 扩大4倍 | C. | 缩小4倍 |
5.下列各式中,( )不是方程.
| A. | x+6<9 | B. | 0.5x=7 | C. | 0.4y-3=9 |
 如图,在梯形ABCD中,上底AB=5厘米,下底DC=8厘米,梯形ABCD的面积是65平方厘米,三角形ABC比三角形ACD小多少平方厘米?
如图,在梯形ABCD中,上底AB=5厘米,下底DC=8厘米,梯形ABCD的面积是65平方厘米,三角形ABC比三角形ACD小多少平方厘米?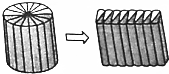 一个圆柱的侧面积与底面积的比是4:1,把这个圆柱沿底面半径分成若干等份,拼成了一个与圆柱等底等高的近似长方体(如图所示),这个近似长方体的底面周长是16.56厘米,原来圆柱的体积是多少立方厘米?
一个圆柱的侧面积与底面积的比是4:1,把这个圆柱沿底面半径分成若干等份,拼成了一个与圆柱等底等高的近似长方体(如图所示),这个近似长方体的底面周长是16.56厘米,原来圆柱的体积是多少立方厘米?