题目内容
7.观察数组:(1),(3、5),(7、9、11),(13、15、17、19),….2011在第( )组.| A. | 44 | B. | 45 | C. | 46 | D. | 无法确定 |
分析 1是第$\frac{1+1}{2}$=1个数、3是第$\frac{3+1}{2}$=2个数、5是第$\frac{5+1}{2}$=3个数…2011是第$\frac{2011+1}{2}$=1006个数.仔细观察不难发现,这是一列相邻奇数,从左到右分组,第一组1个,第二组2个,第三组3个…第n组n个;前一组共1个数,前二组共1+2=3个数,前三级共有1+2+3=6个数…前n项共有1+2+3+…+(n-1)个数,即前n项共有$\frac{n(n+1)}{2}$个数.令$\frac{n(n+1)}{2}$=1006,求n,应用小学知识无法解答,我们令n等于一个值时,求出前n组的个数,再看第1006个数在第几组.
解答 解:$\frac{2011+1}{2}$=$\frac{2012}{2}$=1006
即2011是第1006个数
前n项共有$\frac{n(n+1)}{2}$个数
当n=44时,$\frac{44×(44+1)}{2}$=$\frac{44×45}{2}$=$\frac{1980}{2}$=990
当n=45时$\frac{45×(45+1)}{2}$=$\frac{45×46}{2}$=$\frac{2070}{2}$=1035
990<1006<1035
所以第1006个数在第45组.
故选:B.
点评 此题用小学知识解答比较难,关键是先找出这些数列的规律,确定2011是第几个数,再根据前n项组和的公式看在第几组.

练习册系列答案
相关题目
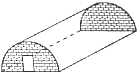 如图,用薄膜盖成的一个蔬菜大棚长12m,它的外形是半个圆柱,两端是半径为3m的半圆形砖墙,盖这个蔬菜大棚至少需要多少平方米的薄膜?(接头损耗忽略不计)
如图,用薄膜盖成的一个蔬菜大棚长12m,它的外形是半个圆柱,两端是半径为3m的半圆形砖墙,盖这个蔬菜大棚至少需要多少平方米的薄膜?(接头损耗忽略不计)