Question

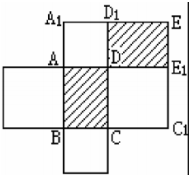长方形ABCD周长为16米，在它的每条边上各画一个以该边为边长的正方形，已知这四个正方形的面积之和是68平方米，求长方形ABCD的面积．（已将辅助图形画好）

Answer 1

分析：根据“长方形ABCD的周长是16厘米”，得出长与宽的和是16÷2=8米，又因BC₁EA₁是正方形，所以BC+CD=BC+CC₁=8米；则BC₁EA₁的面积，利用正方形的面积公式即可求出，而正方形ADD₁A₁的面积与正方形CC₁E₁D的面积和为为4个正方形面积和一半，且长方形ABCD和长方形DE₁ED₁的面积相等，从而可以求出长方形ABCD的面积．

解答：解：因为大正方形BC₁EA₁的边长BC1=BC+CC₁=BC+CD=

1

2

×16=8（米），
所以大正方形BC₁EA₁的面积=8×8=64（平方米）；
又因正方形ADD₁A₁的面积+正方形CC₁E₁D的面积=68÷2=34（平方米），
而长方形ABCD和长方形DE₁ED₁的面积相等，
所以长方形ABCD的面积为（64-34）÷2=15（平方米）；
答：长方形ABCD的面积为15平方米．

点评：解答此题的关键是：先得出大正方形BC₁EA₁的边长，进而求出其面积，从而得到长方形ABCD的面积．