题目内容
各位数字均不大于5,且能被99整除的六位数共有多少个?
考点:数的整除特征
专题:整除性问题
分析:这题直接用排列组合的思路很繁难.计算量非常大.需要转变思路.考虑这样的六位数:ABCD00,它必能被100整除,则六位数ABCD00-四位数ABCD必能被99整除.我们就要找到这样的ABCD,使得ABCD00-ABCD 各位数字不大于5.进一步分类探讨得出答案即可.
解答:
解:设六位数是六位数ABCD00-四位数ABCD必能被99整除.
显然:
1≤A≤5,0≤B≤5.在此基础上:
10-D≤5,得D≥5.
9-C≤5,得4≤C≤9.
D-1-B≤5,得B≥D-6
C-A-1≤5,得A≥C-6
根据上述条件,枚举C、D,并结合A、B的范围,有:
D=5时,B=5、4、3、2、1共5种
D=6时,B=4、3、2、1共4种
D=7时,B=4、3、2共3种
D=8时,B=4、3共2种
D=9时,B=4共1种
C=6时,A=5、4、3、2、1共5种
C=7时,A=5、4、3、2共4种
C=8时,A=5、4、3共3种
C=9时,A=5、4共2种
可知这样的数一共有:
5×6×(5+4+3+2+1)×(5+4+3+2)=6300(种)
答:能被99整除的六位数共有6300个.
显然:
1≤A≤5,0≤B≤5.在此基础上:
10-D≤5,得D≥5.
9-C≤5,得4≤C≤9.
D-1-B≤5,得B≥D-6
C-A-1≤5,得A≥C-6
根据上述条件,枚举C、D,并结合A、B的范围,有:
D=5时,B=5、4、3、2、1共5种
D=6时,B=4、3、2、1共4种
D=7时,B=4、3、2共3种
D=8时,B=4、3共2种
D=9时,B=4共1种
C=6时,A=5、4、3、2、1共5种
C=7时,A=5、4、3、2共4种
C=8时,A=5、4、3共3种
C=9时,A=5、4共2种
可知这样的数一共有:
5×6×(5+4+3+2+1)×(5+4+3+2)=6300(种)
答:能被99整除的六位数共有6300个.
点评:此题考查数的整除特征,注意问题的转化,把问题变得简单易行是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
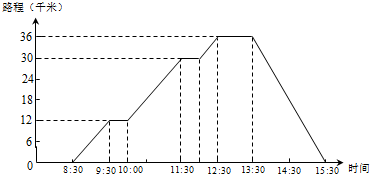 周末李艳和朋友从家出发骑车到红格去玩,请根据统计图回答问题.
周末李艳和朋友从家出发骑车到红格去玩,请根据统计图回答问题. 如图是一张道路图,每段路旁标注的数值表示小悦走这段路所需的分钟数.问:小悦从A出发走到B最快需要多少分钟?
如图是一张道路图,每段路旁标注的数值表示小悦走这段路所需的分钟数.问:小悦从A出发走到B最快需要多少分钟?