题目内容
15．
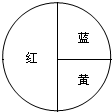看图回答问题四个区域分别为黄、红、蓝色
（1）转动指针，停在黄色、红色、蓝色的区域的可能性各是多少？
黄色：$\frac{1}{4}$
红色：$\frac{1}{2}$
蓝色：$\frac{1}{4}$
（2）如果转动指针100次，估计大约会有多少次指针停在黄色区域里？25．
分析 （1）把整个圆平均分成了4份，红色区域占了2份，黄色区域占了1份，蓝色区域占了1份，求停在红、黄，蓝色区域的可能性，就相当于求1（或2）是4的几分之几，用除法计算；
（2）根据分数乘法的意义，用100乘停在黄色区域的可能性就是指针是停在黄色区域的次数，据此解答．
解答 解：（1）停在黄色区域的可能性是：1÷4=$\frac{1}{4}$，
停在红色区域的可能性是：2÷4=$\frac{1}{2}$，
停在蓝色区域的可能性是：1÷4=$\frac{1}{4}$；
（2）100×$\frac{1}{4}$=25（次），
答：估计大约会有25次指针停在黄色区域里．
故答案为：（1）$\frac{1}{4}$，$\frac{1}{2}$，$\frac{1}{4}$；（2）25．
点评 本题考查了简单事件发生的可能性的求解，即用可能性=所求情况数÷总情况数或求一个数是另一个数的几分之几用除法计算．
练习册系列答案
相关题目
3．口算
| 320÷40= | 60×5= | 200÷50= | 6×23= |
| 68÷17= | 95÷5= | 91÷13= | 560-70= |
10．在○里填＞、＜或=
| $\frac{4}{9}$×$\frac{1}{3}$○$\frac{4}{9}$ | $\frac{3}{4}$÷$\frac{7}{9}$○$\frac{3}{4}$ | 1÷$\frac{2}{3}$○1 |
| $\frac{3}{2}$×$\frac{4}{9}$○$\frac{4}{9}$ | $\frac{5}{9}$×1○1 | $\frac{3}{4}$÷1○$\frac{3}{4}$． |
4．一根长$\frac{4}{5}$米的绳子，截取了$\frac{1}{5}$，还剩（ ）
| A． | 1米 | B． | $\frac{3}{5}$米 | C． | $\frac{16}{25}$米 | D． | $\frac{3}{5}$ |
5．计算题
| $\frac{3}{8}$×101-37.5 | $1\frac{1}{6}$×360÷7 | 4$\frac{4}{5}$×13$\frac{3}{5}$-4$\frac{4}{5}$×3.6 |
| $\frac{25}{4}÷x=\frac{5}{3}$ | $x÷（1-\frac{2}{5}）=3.6$ | 5x-$\frac{5}{6}$=$\frac{5}{12}$ |