题目内容
①
×2003
②
×
+
÷3
③36×
+17×0.25+47×25%
④99×(1-
)×(1-
)×(1-
)×…×(1-
)
⑤
+
+
+
+
+
.
| 2001 |
| 2002 |
②
| 5 |
| 12 |
| 1 |
| 3 |
| 7 |
| 12 |
③36×
| 1 |
| 4 |
④99×(1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 99 |
⑤
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| 30 |
| 1 |
| 42 |
分析:①把2003看作(2002+1),运用乘法分配律简算;
②把除法改为乘法,运用乘法分配律简算;
③把分数和百分数化为小数,运用乘法分配律简算;
④先算出括号内的结果,通过约分计算即可;
⑤通过观察,每个分数都可以分解成两个分数相减的形式,然后通过分数加减相互抵消,求得结果.
②把除法改为乘法,运用乘法分配律简算;
③把分数和百分数化为小数,运用乘法分配律简算;
④先算出括号内的结果,通过约分计算即可;
⑤通过观察,每个分数都可以分解成两个分数相减的形式,然后通过分数加减相互抵消,求得结果.
解答:解:①
×2003,
=
×(2002+1),
=
×2002+
×1,
=2001+
,
=2001
;
②
×
+
÷3,
=
×
+
×
,
=(
+
)×
,
=1×
,
=
;
③36×
+17×0.25+47×25%,
=36×0.25+17×0.25+47×0.25,
=(36+17+47)×0.25,
=100×0.25,
=25;
④99×(1-
)×(1-
)×(1-
)×…×(1-
),
=99×
×
×
×…×
,
=99×
,
=1;
⑤
+
+
+
+
+
,
=1-
+
-
+
-
+
-
+
-
+
-
,
=1-
,
=
.
| 2001 |
| 2002 |
=
| 2001 |
| 2002 |
=
| 2001 |
| 2002 |
| 2001 |
| 2002 |
=2001+
| 2001 |
| 2002 |
=2001
| 2001 |
| 2002 |
②
| 5 |
| 12 |
| 1 |
| 3 |
| 7 |
| 12 |
=
| 5 |
| 12 |
| 1 |
| 3 |
| 7 |
| 12 |
| 1 |
| 3 |
=(
| 5 |
| 12 |
| 7 |
| 12 |
| 1 |
| 3 |
=1×
| 1 |
| 3 |
=
| 1 |
| 3 |
③36×
| 1 |
| 4 |
=36×0.25+17×0.25+47×0.25,
=(36+17+47)×0.25,
=100×0.25,
=25;
④99×(1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 99 |
=99×
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 98 |
| 99 |
=99×
| 1 |
| 99 |
=1;
⑤
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| 30 |
| 1 |
| 42 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 7 |
=1-
| 1 |
| 7 |
=
| 6 |
| 7 |
点评:完成此题,应仔细观察算式特点,运用运算定律或运算技巧,灵活解答.

练习册系列答案
相关题目
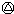 b=(a+b)÷2;若a、b奇偶性不同,则a
b=(a+b)÷2;若a、b奇偶性不同,则a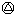 b=(a+b+1)÷2.求(1997
b=(a+b+1)÷2.求(1997 1998)
1998)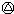 (1998
(1998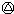 1999)(1999
1999)(1999 2000)
2000)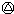 (2000
(2000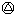 2001)
2001)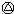 (2001
(2001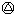 2002)=_
2002)=_