题目内容
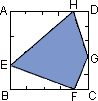 如图,ABCD是面积为1的正方形,AE=2EB,BF=3FC,CG=
如图,ABCD是面积为1的正方形,AE=2EB,BF=3FC,CG=| 2 |
| 3 |
| 1 |
| 5 |
分析:求阴影部分的面积用正方形的面积减去四个空白三角形的面积即可解答.
解答:解:因为AE=2EB,BF=3FC,CG=
GD,DH=
HA,
所以AE=
,EB=
,BF=
,FC=
,CG=
,GD=
,DH=
,HA=
,
所以阴影部分面积=1×1-
×
÷2-
×
÷2-
×
÷2-
×
÷2
=1-
-
-
-
=
.
故答案为:
.
| 2 |
| 3 |
| 1 |
| 5 |
所以AE=
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 1 |
| 6 |
| 5 |
| 6 |
所以阴影部分面积=1×1-
| 2 |
| 3 |
| 5 |
| 6 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 1 |
| 6 |
=1-
| 5 |
| 18 |
| 2 |
| 15 |
| 1 |
| 25 |
| 3 |
| 10 |
=
| 56 |
| 225 |
故答案为:
| 56 |
| 225 |
点评:本题主要考查组合图形的面积,解答此类问题通常将不规则图形转化为规则图形的和或差来解答.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 (2009?崇文区)如图,ABCD是直角梯形,已知OE垂直于DC,AD=10厘米,三角形BOC面积为15平方厘米,那么三角形ADO的面积是
(2009?崇文区)如图,ABCD是直角梯形,已知OE垂直于DC,AD=10厘米,三角形BOC面积为15平方厘米,那么三角形ADO的面积是 (2012?郑州模拟)如图:ABCD是正方形,扇形半径是60毫米,求阴影部分面积.
(2012?郑州模拟)如图:ABCD是正方形,扇形半径是60毫米,求阴影部分面积.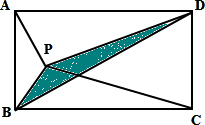 (2004?宜兴市)如图,ABCD是一个长方形.三角形PAB、PBC和PCD的面积分别是44平方厘米,144平方厘米和260平方厘米.图中阴影部分的面积是( )
(2004?宜兴市)如图,ABCD是一个长方形.三角形PAB、PBC和PCD的面积分别是44平方厘米,144平方厘米和260平方厘米.图中阴影部分的面积是( ) 如图,ABCD是正方形,边长是a厘米,BE=
如图,ABCD是正方形,边长是a厘米,BE=