题目内容
如图，若△ABC中，AB=AC，∠BAC=40°，以AB为边，在△ABC的外部作等边△ABD，∠ADC是分析：角度的计算△ABD是等边三角形，那么AB=AD，又AC=AB，得到△ACD是等腰三角形，所以∠DAC=∠DAB+∠BAC=60°+40°=100°，所以∠ADC=（180°-100°）÷2=40°．
解答：解：△ABD是等边三角形，那么AB=AD，又AC=AB，
得到△ACD是等腰三角形，
∠DAC=∠DAB+∠BAC=60°+40°=100°，
所以∠ADC=（180°-100°）÷2=40°．
故答案为：40．
得到△ACD是等腰三角形，
∠DAC=∠DAB+∠BAC=60°+40°=100°，
所以∠ADC=（180°-100°）÷2=40°．
故答案为：40．
点评：本题运用正三角形的意义及等腰三角形的意义进行解答即可．
练习册系列答案
相关题目
如图，在△ABC中，DC=3BD，DE=EA，若△ABC面积是2，则阴影部分的面积是
如图，在△ABC中，BD=5，DE=4，EF=3，FG=2，GC=1，若图中所有三角形面积的和为210平方厘米，那么△ABC的面积为
如图，在△ABC中，已知M、N分别在AC、BC上，BM与AN相交与O．若△AOM，△ABO和△OBN的面积分别是3、2、1．求△MNC的面积．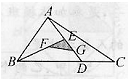
如图，在△ABC中，