题目内容
 如图,矩形ABCD被分成一些正方形.已知AB=32厘米,试求AD的长度是多少?
如图,矩形ABCD被分成一些正方形.已知AB=32厘米,试求AD的长度是多少?分析:可以设最小的正方形的边长为xcm,倒数第二小的正方形边长为ycm,根据DC=AB=32cm,及AD=BC可以得到两个关于xy的方程,解方程组即可,最后求AD的长即可得解.
解答:解:设最小的正方形的边长为xcm,倒数第二小的正方形边长为ycm,根据题意得:
(x+2y)+(x+2y+x)=32
x+2y+y+2y=x+2y+x+
联立求解
解之得:x=4 y=5,
AD=x+2y+y+2y=29cm,
答:AD的长为29cm;
故答案为:29cm.
(x+2y)+(x+2y+x)=32
x+2y+y+2y=x+2y+x+
| x+2y+x+x |
| 2 |
联立求解
解之得:x=4 y=5,
AD=x+2y+y+2y=29cm,
答:AD的长为29cm;
故答案为:29cm.
点评:本题考查了二元一次方程组的应用及学生理解图意的能力,利用二元一次方程组求解的应用题一般情况下题中要给出两个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一个矩形ABCD被分割成九个小矩形,且这些小矩形的面积如图所示,那么矩形ABCD的面积
一个矩形ABCD被分割成九个小矩形,且这些小矩形的面积如图所示,那么矩形ABCD的面积
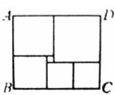 如图所示,矩形ABCD被分割成6个正方形,其中最小正方形的边长等于a,矩形ABCD的面积等于572,则a=
如图所示,矩形ABCD被分割成6个正方形,其中最小正方形的边长等于a,矩形ABCD的面积等于572,则a= 如图,正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形,小正方形的面积的值已标在图中,分别为20和10,18和12,则正方形ABCD和EFGH中,面积较大的正方形是
如图,正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形,小正方形的面积的值已标在图中,分别为20和10,18和12,则正方形ABCD和EFGH中,面积较大的正方形是