Question

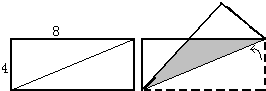已知长方形的长为8，宽为4，将长方形沿一条对角线折起压平，如图所示．求重叠部分（灰色三角形）的面积．

Answer 1

分析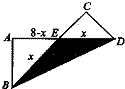：如图所示，因为∠EBD=∠EDB，显然BE=DE，AE=CE设BE=DE=x，则AE=CE=8-x，然后根据勾股定理，求出x的值，进而根据三角形的面积公式求解．

解答：解：如图所示，因为∠EBD=∠EDB，
所以：BE=DE，AE=CE
设BE=DE=x，则
AE=CE=8-x
由勾股定理得：
 （8-x）²+4²=x²
64-16x+x²+16=x²
         16x=80
           x=5；
所以，S_△BDE=

1

2

?BE?CD
=

1

2

×5×4
=10
答：重叠部分的面积是10．

点评：解决本题关键是根据勾股定理求出阴影部分三角形的底，再利用三角形的面积公式求解即可．