题目内容
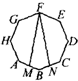 如图,正八边形ABCDEFGH的面积为32平方厘米,M、N分别为AB、BC的中点,则四边形MBNF的面积为
如图,正八边形ABCDEFGH的面积为32平方厘米,M、N分别为AB、BC的中点,则四边形MBNF的面积为8
8
平方厘米.分析:连接点F和B,找出FB的中点O即是正八边形ABCDEFGH的中心,然后连接OM、ON;三角形FMN内的四个小三角形均等底等高,即面积相等,所以三角形MOB的面积=
三角形 FMN;又因为AM=MB,所以三角形MOB的面积=
AOB=
×(
×正八边形ABCDEFGH的面积)=
×(
×32)=2,然后用三角形MOB的面积×4,即可求出四边形MBNF的面积.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
解答: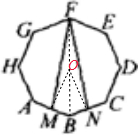 解:如图所示:连接点F和B,找出FB的中点O即是正八边形ABCDEFGH的中心,然后连接OM、ON;
解:如图所示:连接点F和B,找出FB的中点O即是正八边形ABCDEFGH的中心,然后连接OM、ON;
由于FO=OB,所以三角形FMN内的四个小三角形均等底等高,即面积相等,又因为M、N分别为AB、BC的中点,所以三角形MOB的面积=
三角形AOB的面积;
由于点O即是正八边形ABCDEFGH的中心,所以以O为顶点把正八边形看做平均分成了8个三角形,每个三角形占正八边形ABCDEFGH的面积的
,因此三角形AOB的面积=
×正八边形ABCDEFGH的面积=
×32=4(平方厘米);
所以三角形MOB的面积=
三角形AOB的面积=
×4=2(平方厘米);
所以四边形MBNF的面积=三角形MOB的面积×4=2×4=8(平方厘米);
答:则四边形MBNF的面积为8平方厘米.
故答案为:8.
 解:如图所示:连接点F和B,找出FB的中点O即是正八边形ABCDEFGH的中心,然后连接OM、ON;
解:如图所示:连接点F和B,找出FB的中点O即是正八边形ABCDEFGH的中心,然后连接OM、ON;由于FO=OB,所以三角形FMN内的四个小三角形均等底等高,即面积相等,又因为M、N分别为AB、BC的中点,所以三角形MOB的面积=
| 1 |
| 2 |
由于点O即是正八边形ABCDEFGH的中心,所以以O为顶点把正八边形看做平均分成了8个三角形,每个三角形占正八边形ABCDEFGH的面积的
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
所以三角形MOB的面积=
| 1 |
| 2 |
| 1 |
| 2 |
所以四边形MBNF的面积=三角形MOB的面积×4=2×4=8(平方厘米);
答:则四边形MBNF的面积为8平方厘米.
故答案为:8.
点评:利用分割法把四边形MBNF平均分成四个等底等高即面积相等的三角形是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍?
在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍? 请你设计.
请你设计. 如图是一个八边形点阵,中心一个点算是第一层,第二层每边两个点(八边形顶点处有一点为相邻两边公用),第三层每边三个点,第四层每边四个点,其余类推,若八边形点阵共有10层,则点阵中点的总数是
如图是一个八边形点阵,中心一个点算是第一层,第二层每边两个点(八边形顶点处有一点为相邻两边公用),第三层每边三个点,第四层每边四个点,其余类推,若八边形点阵共有10层,则点阵中点的总数是 在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍?
在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍?