Question

快递公司要把3个同样大小的长方体叠在一起打包，并给表面包上牛皮纸，每个长方体的规格如下图．如果要使包装的牛皮纸最省，另外两个应怎样放？请在图中画一画，如果包装的牛皮纸比被包装物体的表面积要大50%，则需要多少平方分米牛皮纸？

Answer 1

考点：长方体、正方体表面积与体积计算的应用

专题：立体图形的认识与计算

分析：根据两个长方体拼组成大长方体的方法，拼在一起的面越小，那么拼组后的大长方体的表面积就越大，反之，拼组后的表面积就越小；所以要使拼成的一个大长方体的表面积最小，只要把两个大面（2×3）叠在一起，减少的4个面积求和解答即可．

解答： 解：画图如下：

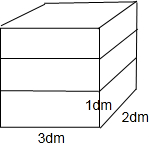
（3×2+3×1+2×1）×2×3-3×2×4
=11×6-24
=42（平方分米）
42×（1+50%）
=42×1.5
=63（平方分米）
答：把另外两个应叠放在上面．需要63平方分米牛皮纸．

点评：解决本题的关键是明确拼组后的长方体的表面积等于这3个小长方体的表面积之和-减少的4个面的面积．