Question

如图，已知点O是三角形ABC内的一点，点O到三边的垂线段的长都为3厘米，三角形ABC的面积为36平方厘米，求三角形ABC的周长．

Answer 1

考点：三角形的周长和面积

专题：平面图形的认识与计算

分析：如图所示，连接OA、OB、OC，则把三角形ABC分成了三个三角形，O点到三条边的垂线就是三个三角形的高，则三个三角形的面积=

1

2

底×高，再把三个三角形面积相加=36平方厘米，即可解答求出大三角形的周长．

解答： 解：

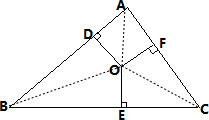
连接OA、OB、OC，
则S△AOB=

1

2

AB×3
S△BOC=

1

2

BC×3
S△AOC=

1

2

AC×3
S△ABC=S△AOB+S△BOC+S△AOC=36
      

1

2

×（AB+BC+AC）×3=36
                 AB+BC+AC=36×

2

3

                 AB+BC+AC=24（厘米）
答：三角形ABC的周长是24厘米．

点评：解答此题的关键是：连接OA、OB、OC，则可知三个小三角形的面积之和=36，进而求出大三角形的周长．