题目内容
 如图,圆O的直径AB与CD互相垂直,AB=10厘米,以C为圆心,CA为半径画弧.求月牙形ADBEA(阴影部分)的面积.
如图,圆O的直径AB与CD互相垂直,AB=10厘米,以C为圆心,CA为半径画弧.求月牙形ADBEA(阴影部分)的面积.分析:如下图所示,图中月牙形ADBEA(阴影部分)的面积=半圆的面积+△ABC的面积-扇形 的面积,其中扇形的面积是以点C为圆心,以AC长为半径的
的面积,其中扇形的面积是以点C为圆心,以AC长为半径的
圆的面积,利用圆及三角形的面积公式求解即可.

 的面积,其中扇形的面积是以点C为圆心,以AC长为半径的
的面积,其中扇形的面积是以点C为圆心,以AC长为半径的| 1 |
| 4 |

解答:解:因为AB与CD是互相垂直的直径,
所以∠ACB是直角,AC=BC.
在直角△ABC中,由勾股定理得,
AC2+BC2=AB2,
则2AC2=102=100,
所以AC2=50.
所以△ABC的面积=
×AC×BC=
×AC2=
×50=25(平方厘米);
扇形 的面积=
的面积=
×π×AC2=
×3.14×50=39.25(平方厘米);
半圆的面积=
×π×(
)2=
×3.14×25=39.25(平方厘米);
所以月牙形ADBEA(阴影部分)的面积=半圆的面积+△ABC的面积-扇形 的面积
的面积
=39.25+25-39.25
=25(平方厘米);
答:月牙形ADBEA的面积是25平方厘米.
所以∠ACB是直角,AC=BC.
在直角△ABC中,由勾股定理得,
AC2+BC2=AB2,
则2AC2=102=100,
所以AC2=50.
所以△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
扇形
 的面积=
的面积=| 1 |
| 4 |
| 1 |
| 4 |
半圆的面积=
| 1 |
| 2 |
| 10 |
| 2 |
| 1 |
| 2 |
所以月牙形ADBEA(阴影部分)的面积=半圆的面积+△ABC的面积-扇形
 的面积
的面积=39.25+25-39.25
=25(平方厘米);
答:月牙形ADBEA的面积是25平方厘米.
点评:本题解决的关键是能用规则图形的面积表示出不规则的月牙形图形的面积.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图所示,圆O的直径AB与CO相互垂直,以C为圆心,CA为半径画弧.其中M和N的面积关系是SM
如图所示,圆O的直径AB与CO相互垂直,以C为圆心,CA为半径画弧.其中M和N的面积关系是SM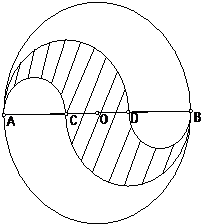 AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积.
AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积.
