题目内容
 如图所示,圆O的直径AB与CO相互垂直,以C为圆心,CA为半径画弧.其中M和N的面积关系是SM
如图所示,圆O的直径AB与CO相互垂直,以C为圆心,CA为半径画弧.其中M和N的面积关系是SM=
=
SN.(>,=,<)分析:设圆的半径为r,则M的面积等于两个直角边长为r的等腰直角三角形面积之和,即2×
×r×r=r2.但这个面积又等于
×AC×BC=
AC2,故AC2=2r2;弯月形N的面积等于,再减去以直角为中心角的扇形CANB的面积,即
×πr2+r2-
×π(2r2)=r2;故弯月形N面积与M面积相等;据此解答.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:根据以上分析知:
设圆的半径是r,
M=2×
×r×r=r2.
又M=
×AC×BC=
AC2,
所以AC2=2r2.
弯月形N面积=半圆ABM的面积+SABC=
×πr2+r2-
×π(2r2)=r2.
所以M的面积等于弯月形N的面积;
故答案为:=.
设圆的半径是r,
M=2×
| 1 |
| 2 |
又M=
| 1 |
| 2 |
| 1 |
| 2 |
所以AC2=2r2.
弯月形N面积=半圆ABM的面积+SABC=
| 1 |
| 2 |
| 1 |
| 4 |
所以M的面积等于弯月形N的面积;
故答案为:=.
点评:本题的关键是根据图形之间的关系,进行分析解答问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

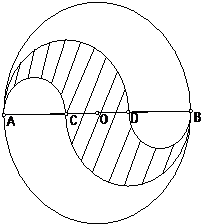 AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积.
AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积. AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积.
AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积.