题目内容
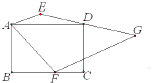长方形ABCD的面积是70平方厘米．梯形AFGE的顶点F在BC上，D是腰EG的中点．试求梯形AFGE的面积．分析：根据题意可连接DF，三角形ADF和长方形ABCD是同底等高的，因此可知三角形ADF的面积是长方形ABCD面积的一半，因为点D是EG的中点，AE平行与FG，所以三角形ADF也是梯形AFGE面积的一半，因为点D是线段EG的中点，所以三角形ADE和三角形DGF的面积就为梯形AFGE面积的一半，即梯形的面积等于长方形的面积，据此解答即可．
解答：解：三角形ADF=70÷2=35（平方厘米），
因为点D为EG的中点，
所以三角形AED+三角形DFG=35（平方厘米），
梯形AFGE的面积：35+35=70（平方厘米），
答：梯形AFGE的面积是70平方厘米．
因为点D为EG的中点，
所以三角形AED+三角形DFG=35（平方厘米），
梯形AFGE的面积：35+35=70（平方厘米），
答：梯形AFGE的面积是70平方厘米．
点评：解答此题的主要依据是三角形的面积是与其等底等高的平行四边形的面积的一半．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
如图，已知长方形ABCD的面积是24平方厘米，三角形ABE的面积是5平方厘米，三角形AFD的面积是6平方厘米，那么三角形AEF的面积是
如图（a），ABCD是一个长方形，其中阴影部分是由一副面积为100平方厘米的七巧版图（b）拼成．那么，长方形ABCD的面积是多少平方厘米？
中间长方形的周长是16米，在它的每条边上画一个以该边为边长的正方形，（如图所示）已知这四个正方形的面积和是68平方米，求长方形ABCD的面积．
如图，已知ABCD和AEFG是两个能完全重合的长方形，且AD边恰好在AE边上，如果BG=18厘米，DE=9厘米，求长方形ABCD的面积．