题目内容
如图，在△ABC中，F是AC的中点，BD=2DC，已知△ABC的面积为36平方厘米．则阴影部分的面积是多少平方厘米？考点：三角形面积与底的正比关系,组合图形的面积
专题：平面图形的认识与计算
分析：连接GC，由图意可以看出，S△BDE=2S△DEC，S△ABE=S△EFC，S△AFB=S△BCF，从而可以推出结果．
解答：
解：如图，连接EC
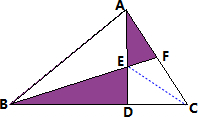
S△BDE=2S△DEC=S2
S△ABE=S3
S△AEF=S△EFC=S1
S△ABF=S△BCF=S1+S3=S1+
S2+S2=36÷2=18
S1+S3=18；S3=3
；
S△ABD=2S△ADC得，
S3+S2=2（S1+S1+
）=36×
=24，
得S2=8，S1=4
则阴影的面积是8+4=12（平方厘米）．
S△BDE=2S△DEC=S2
S△ABE=S3
S△AEF=S△EFC=S1
S△ABF=S△BCF=S1+S3=S1+
| 1 |
| 2 |
S1+S3=18；S3=3
| S2 |
| 2 |
S△ABD=2S△ADC得，
S3+S2=2（S1+S1+
| S2 |
| 2 |
| 2 |
| 3 |
得S2=8，S1=4
则阴影的面积是8+4=12（平方厘米）．
点评：此题主要考查图形面积间的等积代换，三角形的面积与底成正比的关系的灵活应用．
练习册系列答案
相关题目