题目内容
①258÷258
②17
×37-174×1.9+17
×82
③100×(
+
+
+…+
)
| 258 |
| 259 |
②17
| 2 |
| 5 |
| 2 |
| 5 |
③100×(
| 3 |
| 1×4 |
| 3 |
| 4×7 |
| 3 |
| 7×10 |
| 3 |
| 97×100 |
分析:①把带分数化为假分数时,分子不必算出来,其分子部分258×259+258=258×260,其中的258可与被除数中的258约分;
②根据数字特点,原式变为17.4×37-17.4×19+17.4×82,运用乘法分配律简算;
③括号中的每个分数可以拆分为两个分数相减的形式,然后通过加减相抵消的方法,求出结果.
②根据数字特点,原式变为17.4×37-17.4×19+17.4×82,运用乘法分配律简算;
③括号中的每个分数可以拆分为两个分数相减的形式,然后通过加减相抵消的方法,求出结果.
解答:解:①258÷258
,
=258÷
,
=258×
,
=
;
②17
×37-174×1.9+17
×82,
=17.4×37-17.4×19+17.4×82,
=17.4×(37-19+82),
=17.4×100,
=1740;
③100×(
+
+
+…+
),
=100×(1-
+
-
+
-
+…+
-
),
=100×(1-
),
=100×
,
=99.
| 258 |
| 259 |
=258÷
| 258×259+258 |
| 259 |
=258×
| 259 |
| 258×(259+1) |
=
| 259 |
| 260 |
②17
| 2 |
| 5 |
| 2 |
| 5 |
=17.4×37-17.4×19+17.4×82,
=17.4×(37-19+82),
=17.4×100,
=1740;
③100×(
| 3 |
| 1×4 |
| 3 |
| 4×7 |
| 3 |
| 7×10 |
| 3 |
| 97×100 |
=100×(1-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 10 |
| 1 |
| 97 |
| 1 |
| 100 |
=100×(1-
| 1 |
| 100 |
=100×
| 99 |
| 100 |
=99.
点评:解答此题,应注意分析数据,运用运算技巧或运算级定律,进行简算.

练习册系列答案
相关题目
直接写得数:
| 0.24×300= | 4 ×13= ×13= |  ÷ ÷ = = |
| 88÷5= | 1.35× +1.35÷6= +1.35÷6= | 2.6-1 = = |
 ×2÷ ×2÷ ×2= ×2= | (  + + )×4= )×4= | 1.25× ×8= ×8= |
1 +2 +2 ×0= ×0= |
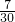 ÷[(
÷[( +
+ -
-