题目内容
已知a÷b=c÷d=27;a=c×3,则b÷d=
3
3
;(a+c)÷(b+d)=27
27
.分析:根据a÷b=c÷d=27,可得b=
,d=
,再根据a=c×3,即可求得b÷d的关系和数值;进而根据b、d的关系和a、c的关系以及c、d的关系,即可求得(a+c)÷(b+d)的数值.
| a |
| 27 |
| c |
| 27 |
解答:解:(1)因为a÷b=c÷d=27,a=c×3,
可得b=
,d=
,
=3
所以b÷d=
÷
=
=3;
(2)因为
=
=3,
可得b=3d,a=3c,
所以(a+c)÷(b+d)=(3c+c)÷(3d+d)=c÷d=27.
故答案为:3,27.
可得b=
| a |
| 27 |
| c |
| 27 |
| a |
| c |
所以b÷d=
| a |
| 27 |
| c |
| 27 |
| a |
| c |
(2)因为
| b |
| d |
| a |
| c |
可得b=3d,a=3c,
所以(a+c)÷(b+d)=(3c+c)÷(3d+d)=c÷d=27.
故答案为:3,27.
点评:解决此题关键是分别把字母b、d用含字母a、c的式子表示出来,进而根据题意得解.

练习册系列答案
相关题目
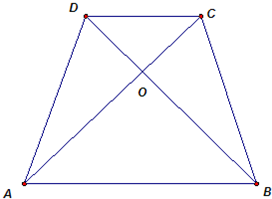 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.