题目内容
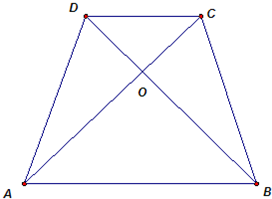 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.分析:要求三角形OAB的面积,可求出三角形OAB的高,如图,过O点做EH垂直于AB、DC,分别交AB、CD于E、H.运用梯形的面积公式,求出EH的长度;然后根据两个三角形的底边与高的比相等,求得OH和OE之间的关系,进而求出0E的长度,解决问题.
解答:解:如图,过O点做EH垂直于AB、DC,分别交AB、CD于E、H,
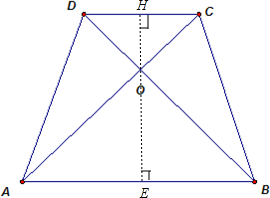
S梯形ABCD=(AB+CD)EH÷2=4,
因为AB=5,CD=3,
所以(5+3)×EH÷2=4,
所以EH=1;
因为
=
=
,
OH=
OE,
OE+OH=EH=1,
所以OE+
OE=1,
因此OE=
,
S△OAB=
×AB×OE=
×5×
=
.
答:三角形OAB的面积是
.

S梯形ABCD=(AB+CD)EH÷2=4,
因为AB=5,CD=3,
所以(5+3)×EH÷2=4,
所以EH=1;
因为
| OE |
| OH |
| AB |
| CD |
| 5 |
| 3 |
OH=
| 3 |
| 5 |
OE+OH=EH=1,
所以OE+
| 3 |
| 5 |
因此OE=
| 5 |
| 8 |
S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 8 |
| 25 |
| 16 |
答:三角形OAB的面积是
| 25 |
| 16 |
点评:此题解答的关键是作出辅助线,求出三角形OAB的高.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目

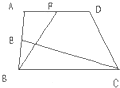 如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为
如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为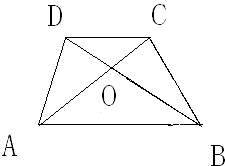 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=6,CD=4,梯形ABCD的面积为5,求三角形OBC的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=6,CD=4,梯形ABCD的面积为5,求三角形OBC的面积.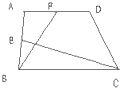 如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为________平方厘米.
如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为________平方厘米.