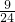题目内容
 如图A、B分别是长方形长和宽的中点,阴影部分的面积是长方形的( )
如图A、B分别是长方形长和宽的中点,阴影部分的面积是长方形的( )分析:如图:设长方形的长为a,宽为b,因为“A、B是长方形长和宽的中点”,所以三角形1的底和高分别是a和
b,三角形2的底和高分别是
a和
b,三角形3的底和高分别是 b和
a,根据三角形的面积公式能算出3个空白三角形部分的面积,则阴影部分的面积=长方形的面积-空白部分的面积,从而找出阴影部分的面积与长方形的面积的百分比.

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

解答:解:长方形的面积是:
a×b=ab,
三角形1的面积是:
×a×
b,
=
ab,
三角形2的面积是:
、
×
a×
b,
=
ab,
三角形3的面积是:
×
a×b,
=
ab,
空白部分的面积是:
ab+
ab+
ab,
=
ab,
阴影部分的面积是:
ab-
ab,
=
ab,
阴影部分的面积是长方形面积的:
ab÷ab=
,
所以阴影部分的面积是长方形面积的
.
故选:A.
a×b=ab,
三角形1的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
三角形2的面积是:
、
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 8 |
三角形3的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
空白部分的面积是:
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
=
| 5 |
| 8 |
阴影部分的面积是:
ab-
| 5 |
| 8 |
=
| 3 |
| 8 |
阴影部分的面积是长方形面积的:
| 3 |
| 8 |
| 3 |
| 8 |
所以阴影部分的面积是长方形面积的
| 3 |
| 8 |
故选:A.
点评:此题主要是先算出3个空白三角形的面积,用长方形的面积减空白部分的面积得阴影部分的面积,再与长方形的面积比.

练习册系列答案
相关题目
 如图,A、B分别是长方形长和宽的中点,那么四边形ABCD占的面积占长方形面积的几分之几?
如图,A、B分别是长方形长和宽的中点,那么四边形ABCD占的面积占长方形面积的几分之几? 如图A、B分别是甲、乙两班学生期末测试成绩统计图,阴影部分表示得优,根据统计图,可知甲班得人优的数相对多一些.
如图A、B分别是甲、乙两班学生期末测试成绩统计图,阴影部分表示得优,根据统计图,可知甲班得人优的数相对多一些. 如图A、B分别是甲、乙两班学生期末测试成绩统计图,阴影部分表示得优,根据统计图,可知甲班得人优的数相对多一些.
如图A、B分别是甲、乙两班学生期末测试成绩统计图,阴影部分表示得优,根据统计图,可知甲班得人优的数相对多一些. 如图A、B分别是长方形长和宽的中点,阴影部分的面积是长方形的
如图A、B分别是长方形长和宽的中点,阴影部分的面积是长方形的