题目内容
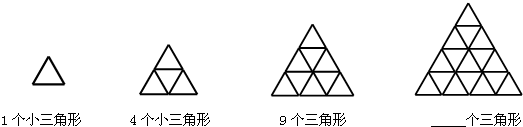
 用火柴棒摆一个三角形要用3根火柴,连摆2个三角形要用5根火柴,连摆3个三角形要用7根火柴(如图所示).如果要连摆m个三角形,要用
用火柴棒摆一个三角形要用3根火柴,连摆2个三角形要用5根火柴,连摆3个三角形要用7根火柴(如图所示).如果要连摆m个三角形,要用分析:搭一个三角形需3根火柴,搭2个三角形中间少用1根,需要5根火柴棒,搭3个三角形中间少用2根,需要7根火柴棒,搭4个三角形中间少用3根,需要9根火柴棒…搭m个三角形中间少用(m-1)根,需要[3m-(m-1)]=2m+1根火柴棒.进而求出有n根火柴(n为大于3的奇数),可连摆几个这样的三角形.
解答:解:(1)搭一个三角形需3根火柴,
搭2个三角形中间少用1根,需要5根火柴棒;
搭3个三角形中间少用2根,需要7根火柴棒;
搭4个三角形中间少用3根,需要9根火柴棒;
所以要连摆m个三角形,要用2m+1根火柴棒;
(2)2m+1=n,
m=(n-1)÷2;
所以有n根火柴(n为大于3的奇数),可连摆(n-1)÷2个这样的三角形;
故答案为:2m+1,(n-1)÷2.
搭2个三角形中间少用1根,需要5根火柴棒;
搭3个三角形中间少用2根,需要7根火柴棒;
搭4个三角形中间少用3根,需要9根火柴棒;
所以要连摆m个三角形,要用2m+1根火柴棒;
(2)2m+1=n,
m=(n-1)÷2;
所以有n根火柴(n为大于3的奇数),可连摆(n-1)÷2个这样的三角形;
故答案为:2m+1,(n-1)÷2.
点评:注意结合图形,发现蕴含的规律,找出解决问题的途径.也可以只分析数字3,5,7,9,11…,得出结论.

练习册系列答案
相关题目
 用火柴棒按下面方式摆三角形,摆一个三角形要3根火柴,摆2个三角形要5根火柴…按这种方式,摆10个三角形要
用火柴棒按下面方式摆三角形,摆一个三角形要3根火柴,摆2个三角形要5根火柴…按这种方式,摆10个三角形要