题目内容
观察下列图形的规律并解答:
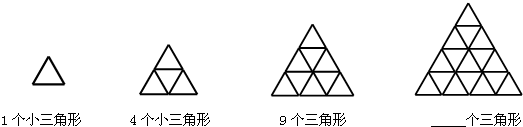
(1)第6个图形中一共有
(2)用三根火柴棒可摆出一个小三角形,那么要摆出第6个图形共需
(3)用三根火柴棒可摆出一个小三角形,现用165根火柴棒摆出具有上面规律的图形,问:这个图形中共有多少个小三角形?

(1)第6个图形中一共有
36
36
个小三角形.(2)用三根火柴棒可摆出一个小三角形,那么要摆出第6个图形共需
63
63
根火柴棒.(3)用三根火柴棒可摆出一个小三角形,现用165根火柴棒摆出具有上面规律的图形,问:这个图形中共有多少个小三角形?
分析:(1)只数小三角形的个数,发现:
1=12,4=22,9=32;…
第n个图形中,小三角形的个数是n的平方;
(2)第1个图形中需要1×3根,第2个图形中需要1×3+2×3根,以此类推,第n个图形中,需要1×3+2×+3×3+…+n×3=3(1+2+3+…+n)=
根;由此把n=6代入计算即可;
(3)令
=165,由此求出n的取值,然后再求出它的平方数即可.
1=12,4=22,9=32;…
第n个图形中,小三角形的个数是n的平方;
(2)第1个图形中需要1×3根,第2个图形中需要1×3+2×3根,以此类推,第n个图形中,需要1×3+2×+3×3+…+n×3=3(1+2+3+…+n)=
| 3n(1+n) |
| 2 |
(3)令
| 3n(1+n) |
| 2 |
解答:解:(1)62=36(个);
答:第6个图形中一共有36个小三角形.
(2)
,
=
,
=3×3×7,
=63(根);
答:要摆出第6个图形共需63根火柴棒.
(3)
=165,
3n(1+n)=330,
n(1+n)=110,
因为10×11=110;
所以n=10;
102=100(个);
答:这个图形中共有100个小三角形.
答:第6个图形中一共有36个小三角形.
(2)
| 3n(1+n) |
| 2 |
=
| 3×6×(1+6) |
| 2 |
=3×3×7,
=63(根);
答:要摆出第6个图形共需63根火柴棒.
(3)
| 3n(1+n) |
| 2 |
3n(1+n)=330,
n(1+n)=110,
因为10×11=110;
所以n=10;
102=100(个);
答:这个图形中共有100个小三角形.
点评:此类题要首先正确数出特例中的数据,进一步发现数据之间的关系,归纳出通项即可.

练习册系列答案
相关题目