题目内容
如图,三个半径都是2厘米的圆两两相交于圆心,阴影部分的面积是多少平方厘米?


考点:组合图形的面积
专题:几何的计算与计数专题
分析:如图所示,连接其中一个阴影部分的三点构成一个等边三角形,从图中你会发现:每一块阴影部分面积=正三角形面积+两个弓形面积-一个弓形面积=扇形面积.所以我们可以求出以这个以这个小阴影部分为主的扇形面积=
cm2,再乘3,就是阴影的总面积.
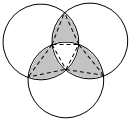
| 60×π×22 |
| 360 |

解答:
解:S阴影=3×S扇形
=3×=
=3×
=6.28(平方厘米)
答:阴影部分的面积是6.28平方厘米.
=3×=
| 60×π×22 |
| 360 |
=3×
| 6.28 |
| 3 |
=6.28(平方厘米)
答:阴影部分的面积是6.28平方厘米.
点评:本题的关键是看出每一块阴影部分面积=正三角形面积+两个弓形面积-一个弓形面积,即一个圆心角为60°的扇形的面积.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目


 李大爷家有一块菜地.(形状如图,单位米)
李大爷家有一块菜地.(形状如图,单位米)