题目内容
15.已知:AB∥CD,CE、AE分别平分∠ACD、∠CAB,求∠1+∠2=90°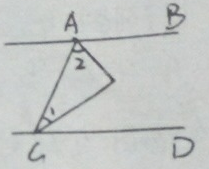
分析 根据两直线平行,同旁内角互补可得∠BAC+∠ACD=180°,根据角平分线的定义可得∠1=$\frac{1}{2}$∠BAC,∠2=$\frac{1}{2}$∠ACD,然后整理即可得解.
解答 解:因为AB∥CD,
所以∠BAC+∠ACD=180°,
因为AE平分∠BAC,CE平分∠ACD,
所以∠1=$\frac{1}{2}$∠BAC,∠2=$\frac{1}{2}$∠ACD,
所以∠1+∠2=$\frac{1}{2}$(∠BAC+∠ACD)=$\frac{1}{2}$×180°=90°.
故答案为:90°.
点评 本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.哪把钥匙能开万宝箱?( )


| A. |  | B. |  | ||
| C. |  | D. |  |
4.将直角三角形ABC以BC为轴旋转一周,得到的圆锥体积是V,那么V=( )


| A. | 16π | B. | 12π | C. | 25π | D. | 48π |
5.计算下面各题,能简算的要简算.
| 52×101 | 90.5×99+90.5 | 12×($\frac{1}{4}$+$\frac{1}{2}$-$\frac{1}{3}$) |
| $\frac{3}{7}$÷$\frac{5}{6}$+$\frac{4}{7}$×$\frac{6}{5}$ | 0.7÷[($\frac{5}{6}$-$\frac{1}{4}$)×24] | $\frac{7}{11}÷[{\frac{2}{5}-({1-\frac{7}{10}})}]$ |